Understanding traverse and sequence

This post is one in a series. In the first two posts, I described some of the core functions for dealing with generic data types: map, bind, and so on. In the previous post, I discussed “applicative” vs “monadic” style, and how to lift values and functions to be consistent with each other.

In this post, we’ll look at a common problem: working with lists of elevated values.

Here’s a list of shortcuts to the various functions mentioned in this series:

• Part 1: Lifting to the elevated world
  • The map function
  • The return function
  • The apply function
  • The liftN family of functions
  • The zip function and ZipList world
• Part 2: How to compose world-crossing functions
  • The bind function
  • List is not a monad. Option is not a monad.
• Part 3: Using the core functions in practice
  • Independent and dependent data
  • Example: Validation using applicative style and monadic style
  • Lifting to a consistent world
  • Kleisli world
• Part 4: Mixing lists and elevated values
  • Mixing lists and elevated values
  • The traverse/MapM function
  • The sequence function
  • “Sequence” as a recipe for ad-hoc implementations
  • Readability vs. performance
  • Dude, where’s my filter?
• Part 5: A real-world example that uses all the techniques
  • Example: Downloading and processing a list of websites
  • Treating two worlds as one
• Part 6: Designing your own elevated world
  • Designing your own elevated world
  • Filtering out failures
  • The Reader monad
• Part 7: Summary
  • List of operators mentioned
  • Further reading

A common issue is how to deal with lists or other collections of elevated values.

Here are some examples:

• Example 1: We have a parseInt with signature string -> int option, and we have a list of strings. We want to parse all the strings at once. Now of course we can use map to convert the list of strings to a list of options. But what we really want is not a “list of options” but an “option of list”, a list of parsed ints, wrapped in an option in case any fail.

• Example 2: We have a readCustomerFromDb function with signature CustomerId -> Result<Customer>, that will return Success if the record can be found and returned, and Failure otherwise. And say we have a list of CustomerIds and we want to read all the customers at once. Again, we can use map to convert the list of ids to a list of results. But what we really want is not a list of Result<Customer>, but a Result containing a Customer list, with the Failure case in case of errors.

• Example 3: We have a fetchWebPage function with signature Uri -> Async<string>, that will return a task that will download the page contents on demand. And say we have a list of Uriss and we want to fetch all the pages at once. Again, we can use map to convert the list of Uris to a list of Asyncs. But what we really want is not a list of Async, but a Async containing a list of strings.

Let’s start by coming up with a solution for the first case and then seeing if we can generalize it to the others.

The obvious approach would be:

• First, use map to turn the list of string into a list of Option<int>.
• Next, create a function that turns the list of Option<int> into an Option<int list>.

But this requires two passes through the list. Can we do it in one pass?

Yes! If we think about how a list is built, there is a “cons” function (:: in F#) that is used to join the head to the tail. If we elevate this to the Option world, we can use Option.apply to join a head Option to a tail Option using the lifted version of cons.

let (<*>) = Option.apply
let retn = Some

let rec mapOption f list =
    let cons head tail = head :: tail
    match list with
    | [] ->
        retn []
    | head::tail ->
        retn cons <*> (f head) <*> (mapOption f tail)

NOTE: I defined cons explicitly because :: is not a function and List.Cons takes a tuple and is thus not usable in this context.

Here is the implementation as a diagram:

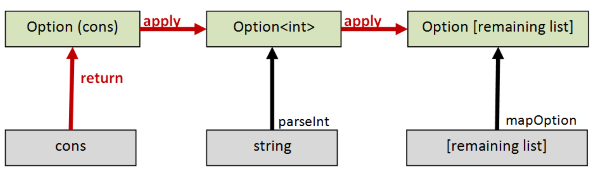
If you are confused as to how this works, please read the section on apply in the first post in this series.

Note also that I am explicitly defining retn and using it in the implementation rather than just using Some. You’ll see why in the next section.

Now let’s test it!

let parseInt str =
    match (System.Int32.TryParse str) with
    | true,i -> Some i
    | false,_ -> None
// string -> int option

let good = ["1";"2";"3"] |> mapOption parseInt
// Some [1; 2; 3]

let bad = ["1";"x";"y"] |> mapOption parseInt
// None

We start by defining parseInt of type string -> int option (piggybacking on the existing .NET library).

We use mapOption to run it against a list of good values, and we get Some [1; 2; 3], with the list inside the option, just as we want.

And if we use a list where some of the values are bad, we get None for the entire result.

Let’s repeat this, but this time using the Result type from the earlier validation example.

Here’s the mapResult function:

let (<*>) = Result.apply
let retn = Success

let rec mapResult f list =
    let cons head tail = head :: tail
    match list with
    | [] ->
        retn []
    | head::tail ->
        retn cons <*> (f head) <*> (mapResult f tail)

Again I am explicitly defining a retn rather than just using Success. And because of this, the body of the code for mapResult and mapOption is exactly the same!

Now let’s change parseInt to return a Result rather than an Option:

let parseInt str =
    match (System.Int32.TryParse str) with
    | true,i -> Success i
    | false,_ -> Failure [str + " is not an int"]

And then we can rerun the tests again, but this time getting more informative errors in the failure case:

let good = ["1";"2";"3"] |> mapResult parseInt
// Success [1; 2; 3]

let bad = ["1";"x";"y"] |> mapResult parseInt
// Failure ["x is not an int"; "y is not an int"]

The implementations of mapOption and mapResult have exactly the same code, the only difference is the different retn and <*> functions (from Option and Result, respectively).

So the question naturally arises, rather than having mapResult, mapOption, and other specific implementations for each elevated type, can we make a completely generic version of mapXXX that works for all elevated types?

The obvious thing would be able to pass these two functions in as an extra parameter, like this:

let rec mapE (retn,ap) f list =
    let cons head tail = head :: tail
    let (<*>) = ap

    match list with
    | [] ->
        retn []
    | head::tail ->
        (retn cons) <*> (f head) <*> (mapE retn ap f tail)

There are some problems with this though. First, this code doesn’t compile in F#! But even if it did, we’d want to make sure that the same two parameters were passed around everywhere.

We might attempt this by creating a record structure containing the two parameters, and then create one instance for each type of elevated world:

type Applicative<'a,'b> = {
    retn: 'a -> E<'a>
    apply: E<'a->'b> -> E<'a> -> E<'b>
    }

// functions for applying Option
let applOption = {retn = Option.Some; apply=Option.apply}

// functions for applying Result
let applResult = {retn = Result.Success; apply=Result.apply}

The instance of the Applicative record (appl say) would be an extra parameter to our generic mapE function, like this:

let rec mapE appl f list =
    let cons head tail = head :: tail
    let (<*>) = appl.apply
    let retn = appl.retn

    match list with
    | [] ->
        retn []
    | head::tail ->
        (retn cons) <*> (f head) <*> (mapE retn ap f tail)

In use, we would pass in the specific applicative instance that we want, like this:

// build an Option specific version...
let mapOption = mapE applOption

// ...and use it
let good = ["1";"2";"3"] |> mapOption parseInt

Unfortunately, none of this works either, at least in F#. The Applicative type, as defined, won’t compile. This is because F# does not support “higher-kinded types”. That is, we can’t parameterize the Applicative type with a generic type, only with concrete types.

In Haskell and languages that do support “higher-kinded types”, the Applicative type that we’ve defined is similar to a “type class”. What’s more, with type classes, we don’t have to pass around the functions explicitly – the compiler will do that for us.

There is actually a clever (and hacky) way of getting the same effect in F# though using static type constraints. I’m not going to discuss it here, but you can see it used in the FSharpx library.

The alternative to all this abstraction is just creating a mapXXX function for each elevated world that we want to work with: mapOption, mapResult, mapAsync and so on.

Personally I am OK with this cruder approach. There are not that many elevated worlds that you work with regularly, and even though you lose out on abstraction, you gain on explicitness, which is often useful when working in a team of mixed abilities.

So let’s look at these mapXXX functions, also called traverse.

Common Names: mapM, traverse, for

Common Operators: None

What it does: Transforms a world-crossing function into a world-crossing function that works with collections

Signature: (a->E<b>) -> a list -> E<b list> (or variants where list is replaced with other collection types)

We saw above that we can define a set of mapXXX functions, where XXX stands for an applicative world – a world that has apply and return. Each of these mapXXX functions transforms a world-crossing function into a world-crossing function that works with collections.

And as we noted above, if the language supports type classes, we can get away with a single implementation, called mapM or traverse. I’m going to call the general concept traverse from now on to make it clear that is different from map.

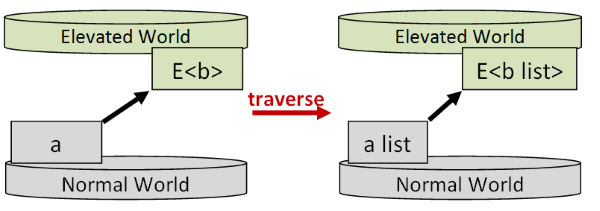
Understanding the difference between map and traverse can be hard, so let’s see if we can explain it in pictures.

First, let’s introduce some visual notation using the analogy of an “elevated” world sitting above a “normal” world.

Some of these elevated worlds (in fact almost all of them!) have apply and return functions. We’ll call these “Applicative worlds”. Examples include Option, Result, Async, etc.

And some of these elevated worlds have a traverse function. We’ll call these “Traversable worlds”, and we’ll use List as a classic example.

If a Traversable world is on top, that produces a type such as List<a>, and if an Applicative world is on top, that produces a type such as Result<a>.

IMPORTANT: I will be using the syntax List<_> to represent “List world” for consistency with Result<_>, etc. This is not meant to be the same as the .NET List class! In F#, this would be implemented by the immutable list type.

But from now on we are going to be dealing with both kinds of elevated worlds in the same “stack”.

The Traversable world can be stacked on top of the Applicative world, which produces a type such as List<Result<a>>, or alternatively, the Applicative world world can be stacked on top of the Traversable world, which produces a type such as Result<List<a>>.

Now let’s see what the different kinds of functions look like using this notation.

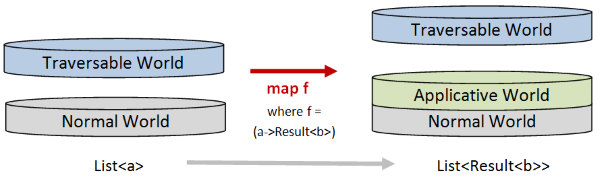
Let’s start with a plain cross-world function such as a -> Result<b>, where the target world is an applicative world. In the diagram, the input is a normal world (on the left), and the output (on the right) is an applicative world stacked on top of the normal world.

Now if we have a list of normal a values, and then we use map to transform each a value using a function like a -> Result<b>, the result will also be a list, but where the contents are Result<b> values instead of a values.

When it comes to traverse the effect is quite different. If we use traverse to transform a list of a values using that function, the output will be a Result, not a list. And the contents of the Result will be a List<b>.

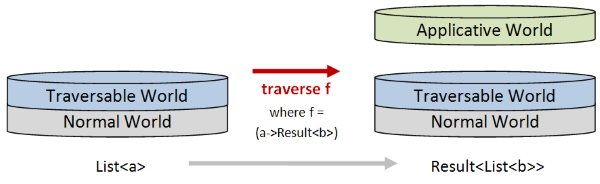
In other words, with traverse, the List stays attached to the normal world, and the Applicative world (such as Result) is added at the top.

Ok, I know this all sounds very abstract, but it is actually a very useful technique. We’ll see an example of this is used in practice below.

It turns out that traverse can be implemented in an applicative style or a monadic style, so there are often two separate implementations to choose from. The applicative versions tend to end in A and the monadic versions end in M, which is helpful!

Let’s see how this works with our trusty Result type.

First, we’ll implement traverseResult using both applicative and monadic approaches.

module List =

    /// Map a Result producing function over a list to get a new Result
    /// using applicative style
    /// ('a -> Result<'b>) -> 'a list -> Result<'b list>
    let rec traverseResultA f list =

        // define the applicative functions
        let (<*>) = Result.apply
        let retn = Result.Success

        // define a "cons" function
        let cons head tail = head :: tail

        // loop through the list
        match list with
        | [] ->
            // if empty, lift [] to a Result
            retn []
        | head::tail ->
            // otherwise lift the head to a Result using f
            // and cons it with the lifted version of the remaining list
            retn cons <*> (f head) <*> (traverseResultA f tail)


    /// Map a Result producing function over a list to get a new Result
    /// using monadic style
    /// ('a -> Result<'b>) -> 'a list -> Result<'b list>
    let rec traverseResultM f list =

        // define the monadic functions
        let (>>=) x f = Result.bind f x
        let retn = Result.Success

        // define a "cons" function
        let cons head tail = head :: tail

        // loop through the list
        match list with
        | [] ->
            // if empty, lift [] to a Result
            retn []
        | head::tail ->
            // otherwise lift the head to a Result using f
            // then lift the tail to a Result using traverse
            // then cons the head and tail and return it
            f head                 >>= (fun h ->
            traverseResultM f tail >>= (fun t ->
            retn (cons h t) ))

The applicative version is the same implementation that we used earlier.

The monadic version applies the function f to the first element and then passes it to bind. As always with monadic style, if the result is bad the rest of the list will be skipped.

On the other hand, if the result is good, the next element in the list is processed, and so on. Then the results are cons’ed back together again.

NOTE: These implementations are for demonstration only! Neither of these implementations are tail-recursive, and so they will fail on large lists!

Alright, let’s test the two functions and see how they differ. First we need our parseInt function:

/// parse an int and return a Result
/// string -> Result<int>
let parseInt str =
    match (System.Int32.TryParse str) with
    | true,i -> Result.Success i
    | false,_ -> Result.Failure [str + " is not an int"]

Now if we pass in a list of good values (all parsable), the result for both implementations is the same.

// pass in strings wrapped in a List
// (applicative version)
let goodA = ["1"; "2"; "3"] |> List.traverseResultA parseInt
// get back a Result containing a list of ints
// Success [1; 2; 3]

// pass in strings wrapped in a List
// (monadic version)
let goodM = ["1"; "2"; "3"] |> List.traverseResultM parseInt
// get back a Result containing a list of ints
// Success [1; 2; 3]

But if we pass in a list with some bad values, the results differ.

// pass in strings wrapped in a List
// (applicative version)
let badA = ["1"; "x"; "y"] |> List.traverseResultA parseInt
// get back a Result containing a list of ints
// Failure ["x is not an int"; "y is not an int"]

// pass in strings wrapped in a List
// (monadic version)
let badM = ["1"; "x"; "y"] |> List.traverseResultM parseInt
// get back a Result containing a list of ints
// Failure ["x is not an int"]

The applicative version returns all the errors, while the monadic version returns only the first error.

I mentioned above that the “from-scratch” implementation was not tail recursive and would fail for large lists. That could be fixed of course, at the price of making the code more complicated.

On the other hand, if your collection type has a “right fold” function, as List does, then you can use that to make the implementation simpler, faster, and safer too.

In fact, I always like to use fold and its ilk wherever possible so that I never have to worry about getting tail-recursion right!

So, here are the re-implementations of traverseResult, using List.foldBack. I have kept the code as similar as possible, but delegated the looping over the list to the fold function, rather than creating a recursive function.

/// Map a Result producing function over a list to get a new Result
/// using applicative style
/// ('a -> Result<'b>) -> 'a list -> Result<'b list>
let traverseResultA f list =

    // define the applicative functions
    let (<*>) = Result.apply
    let retn = Result.Success

    // define a "cons" function
    let cons head tail = head :: tail

    // right fold over the list
    let initState = retn []
    let folder head tail =
        retn cons <*> (f head) <*> tail

    List.foldBack folder list initState

/// Map a Result producing function over a list to get a new Result
/// using monadic style
/// ('a -> Result<'b>) -> 'a list -> Result<'b list>
let traverseResultM f list =

    // define the monadic functions
    let (>>=) x f = Result.bind f x
    let retn = Result.Success

    // define a "cons" function
    let cons head tail = head :: tail

    // right fold over the list
    let initState = retn []
    let folder head tail =
        f head >>= (fun h ->
        tail >>= (fun t ->
        retn (cons h t) ))

    List.foldBack folder list initState

Note that this approach will not work for all collection classes. Some types do not have a right fold, so traverse must be implemented differently.

All these examples have used the list type as the collection type. Can we implement traverse for other types too?

Yes. For example, an Option can be considered a one-element list, and we can use the same trick.

For example, here’s an implementation of traverseResultA for Option

module Option =

    /// Map a Result producing function over an Option to get a new Result
    /// ('a -> Result<'b>) -> 'a option -> Result<'b option>
    let traverseResultA f opt =

        // define the applicative functions
        let (<*>) = Result.apply
        let retn = Result.Success

        // loop through the option
        match opt with
        | None ->
            // if empty, lift None to an Result
            retn None
        | Some x ->
            // lift value to an Result
            (retn Some) <*> (f x)

Now we can wrap a string in an Option and use parseInt on it. Rather than getting a Option of Result, we invert the stack and get a Result of Option.

// pass in an string wrapped in an Option
let good = Some "1" |> Option.traverseResultA parseInt
// get back a Result containing an Option
// Success (Some 1)

If we pass in an unparsable string, we get failure:

// pass in an string wrapped in an Option
let bad = Some "x" |> Option.traverseResultA parseInt
// get back a Result containing an Option
// Failure ["x is not an int"]

If we pass in None, we get Success containing None!

// pass in an string wrapped in an Option
let goodNone = None |> Option.traverseResultA parseInt
// get back a Result containing an Option
// Success (None)

This last result might be surprising at first glance, but think of it this way, the parsing didn’t fail, so there was no Failure at all.

Types that can implement a function like mapXXX or traverseXXX are called Traversable. For example, collection types are Traversables as well as some others.

As we saw above, in a language with type classes a Traversable type can get away with just one implementation of traverse, but in a language without type classes a Traversable type will need one implementation per elevated type.

Also note that, unlike all the generic functions we have created before, the type being acted on (inside the collection) must have appropriate apply and return functions in order for traverse to be implemented. That is, the inner type must be an Applicative.

As always, a correct implementation of traverse should have some properties that are true no matter what elevated world we are working with.

These are the “Traversable Laws”, and a Traversable is defined as a generic data type constructor – E<T> – plus a set of functions (traverse or traverseXXX ) that obey these laws.

The laws are similar to the previous ones. For example, the identity function should be mapped correctly, composition should be preserved, etc.

Common Names: sequence

Common Operators: None

What it does: Transforms a list of elevated values into an elevated value containing a list

Signature: E<a> list -> E<a list> (or variants where list is replaced with other collection types)

We saw above how you can use the traverse function as a substitute for map when you have a function that generates an applicative type such as Result.

But what happens if you are just handed a List<Result> and you need to change it to a Result<List>. That is, you need to swap the order of the worlds on the stack:

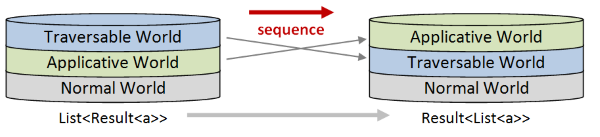
This is where sequence is useful – that’s exactly what it does! The sequence function “swaps layers”.

The order of swapping is fixed:

• The Traversable world starts higher and is swapped down.
• The Applicative world starts lower and is swapped up.

Note that if you already have an implementation of traverse, then sequence can be derived from it easily. In fact, you can think of sequence as traverse with the id function baked in.

Just as with traverse, there can be applicative and monadic versions of sequence:

• sequenceA for the applicative one.
• sequenceM (or just sequence) for the monadic one.

Let’s implement and test a sequence implementation for Result:

module List =

    /// Transform a "list<Result>" into a "Result<list>"
    /// and collect the results using apply
    /// Result<'a> list -> Result<'a list>
    let sequenceResultA x = traverseResultA id x

    /// Transform a "list<Result>" into a "Result<list>"
    /// and collect the results using bind.
    /// Result<'a> list -> Result<'a list>
    let sequenceResultM x = traverseResultM id x

Ok, that was too easy! Now let’s test it, starting with the applicative version:

let goodSequenceA =
    ["1"; "2"; "3"]
    |> List.map parseInt
    |> List.sequenceResultA
// Success [1; 2; 3]

let badSequenceA =
    ["1"; "x"; "y"]
    |> List.map parseInt
    |> List.sequenceResultA
// Failure ["x is not an int"; "y is not an int"]

and then the monadic version:

let goodSequenceM =
    ["1"; "2"; "3"]
    |> List.map parseInt
    |> List.sequenceResultM
// Success [1; 2; 3]

let badSequenceM =
    ["1"; "x"; "y"]
    |> List.map parseInt
    |> List.sequenceResultM
// Failure ["x is not an int"]

As before, we get back a Result<List>, and as before the monadic version stops on the first error, while the applicative version accumulates all the errors.

We saw above that having type classes like Applicative means that you only need to implement traverse and sequence once. In F# and other languages without high-kinded types you have to create an implementation for each type that you want to traverse over.

Does that mean that the concepts of traverse and sequence are irrelevant or too abstract? I don’t think so.

Instead of thinking of them as library functions, I find that it is useful to think of them as recipes – a set of instructions that you can follow mechanically to solve a particular problem.

In many cases, the problem is unique to a context, and there is no need to create a library function – you can create a helper function as needed.

Let me demonstrate with an example. Say that you are given a list of options, where each option contains a tuple, like this:

let tuples = [Some (1,2); Some (3,4); None; Some (7,8);]
// List<Option<Tuple<int>>>

This data is in the form List<Option<Tuple<int>>>. And now say, that for some reason, you need to turn it into a tuple of two lists, where each list contains options, like this:

let desiredOutput = [Some 1; Some 3; None; Some 7],[Some 2; Some 4; None; Some 8]
// Tuple<List<Option<int>>>

The desired result is in the form Tuple<List<Option<int>>>.

So, how would you write a function to do this? Quick!

No doubt you could come up with one, but it might require a bit of thought and testing to be sure you get it right.

On the other hand, if you recognize that this task is just transforming a stack of worlds to another stack, you can create a function mechanically, almost without thinking.

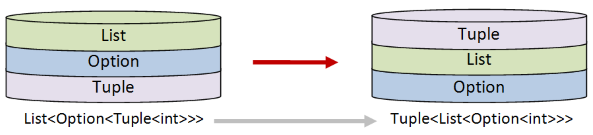
To design the solution, we need to pay attention to which worlds move up and which worlds move down.

• The tuple world needs to end up at the top, so it will have to be swapped “up”, which in turn means that it will play the role of “applicative”.
• The option and list worlds need to be swapped “down”, which in turn means that they will both play the role of “traversable”.

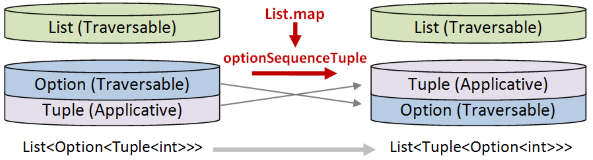
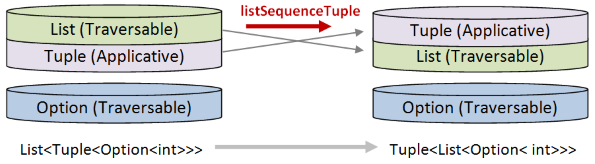
In order to do this transform then, I will need two helper functions:

• optionSequenceTuple will move an option down and a tuple up.

• listSequenceTuple will move a list down and a tuple up.

Do these helper functions need to be in a library? No. It’s unlikely that I will need them again, and even I need them occasionally, I’d prefer to write them scratch to avoid having to take a dependency.

On the other hand, the List.sequenceResult function implemented earlier that converts a List<Result<a>> to a Result<List<a>> is something I do use frequently, and so that one is worth centralizing.

Once we know how the solution will look, we can start coding mechanically.

First, the tuple is playing the role of the applicative, so we need to define the apply and return functions:

let tupleReturn x = (x, x)
let tupleApply (f,g) (x,y) = (f x, g y)

Next, define listSequenceTuple using exactly the same right fold template as we did before, with List as the traversable and tuple as the applicative:

let listSequenceTuple list =
    // define the applicative functions
    let (<*>) = tupleApply
    let retn = tupleReturn

    // define a "cons" function
    let cons head tail = head :: tail

    // right fold over the list
    let initState = retn []
    let folder head tail = retn cons <*> head <*> tail

    List.foldBack folder list initState

There is no thinking going on here. I’m just following the template!

We can test it immediately:

[ (1,2); (3,4)] |> listSequenceTuple
// Result => ([1; 3], [2; 4])

And it gives a tuple with two lists, as expected.

Similarly, define optionSequenceTuple using the same right fold template again. This time Option is the traversable and tuple is still the applicative:

let optionSequenceTuple opt =
    // define the applicative functions
    let (<*>) = tupleApply
    let retn = tupleReturn

    // right fold over the option
    let initState = retn None
    let folder x _ = (retn Some) <*> x

    Option.foldBack folder opt initState

We can test it too:

Some (1,2) |> optionSequenceTuple
// Result => (Some 1, Some 2)

And it gives a tuple with two options, as expected.

Finally, we can glue all the parts together. Again, no thinking required!

let convert input =
    input

    // from List<Option<Tuple<int>>> to List<Tuple<Option<int>>>
    |> List.map optionSequenceTuple

    // from List<Tuple<Option<int>>> to Tuple<List<Option<int>>>
    |> listSequenceTuple

And if we use it, we get just what we wanted:

let output = convert tuples
// ( [Some 1; Some 3; None; Some 7], [Some 2; Some 4; None; Some 8] )

output = desiredOutput |> printfn "Is output correct? %b"
// Is output correct? true

Ok, this solution is more work than having one reusable function, but because it is mechanical, it only takes a few minutes to code, and is still easier than trying to come up with your own solution!

Want more? For an example of using sequence in a real-world problem, please read this post.

At the beginning of this post I noted our tendency as functional programmers to map first and ask questions later.

In other words, given a Result producing function like parseInt, we would start by collecting the results and only then figure out how to deal with them. Our code would look something like this, then:

["1"; "2"; "3"]
|> List.map parseInt
|> List.sequenceResultM

But of course, this does involve two passes over the list, and we saw how traverse could combine the map and the sequence in one step, making only one pass over the list, like this:

["1"; "2"; "3"]
|> List.traverseResultM parseInt

So if traverse is more compact and potentially faster, why ever use sequence?

Well, sometimes you are given a certain structure and you have no choice, but in other situations I might still prefer the two-step map-sequence approach just because it is easier to understand. The mental model for “map” then “swap” seems easier to grasp for most people than the one-step traverse.

In other words, I would always go for readability unless you can prove that performance is impacted. Many people are still learning FP, and being overly cryptic is not helpful, in my experience.

We’ve seen that functions like map and sequence work on lists to transform them into other types, but what about filtering? How can I filter things using these methods?

The answer is – you can’t! map, and traverse and sequence are all “structure preserving”. If you start with a list of 10 things you still have a list of 10 things afterwards, albeit somewhere else in the stack. Or if you start with a tree with three branches, you still have a tree of three branches at the end.

In the tuple example above, the original list had four elements, and after the transformation, the two new lists in the tuple also had four elements.

If you need to change the structure of a type, you need to use something like fold. Fold allows you to build a new structure from an old one, which means that you can use it to create a new list with some elements missing (i.e. a filter).

The various uses of fold are worthy of their own series, so I’m going to save a discussion of filtering for another time.

In this post, we learned about traverse and sequence as a way of working with lists of elevated values.

In the next post we’ll finish up by working through a practical example that uses all the techniques that have been discussed.