The EDFH is defeated once again

In the first post in this series, we came up with some properties that could be used to test a run-length encoding implementation:

• The output must contain all the characters from the input, in the same order
• Two adjacent characters in the output cannot be the same
• The sum of the run lengths in the output must equal the total length of the input
• If the input is reversed, the output must also be reversed

In the previous post, we tested various RLE implementations created by the Enterprise Developer From Hell and were happy that they all failed.

But are these four properties enough to correctly check a RLE implementation? Can the EDFH create a implementation that would satisfy these properties and yet be wrong?

The answer is yes! The EDFH can take the output of a correct implementation and then add some extra characters to the beginning and end of the list to corrupt the answer. Exactly what things to add are constrained by the properties above:

• The “two adjacent characters” property means that the new prefix has to be different from the first character.
• But the “all the characters in the same order” property means that the EDFH can’t just add a different character because that would break the “in same order”. The workaround is that the EDFH adds a duplicate of the first two characters!
• The “sum of the run lengths” property means that the run-lengths for the new prefix must steal a count from subsequent runs. If we didn’t steal a count, and used 0 as a run-length for these new elements, then that would actually be an acceptable RLE – not corrupt at all!
• And finally, the “reversed” property means the both the front and the rear of the list must be modified in the same way. To avoid corrupting the same elements twice, we require the list to have at least four elements.

Putting all those requirements together, we can come up with this implementation, where rle_recursive is the correct RLE implementation from the previous post.

/// An incorrect implementation that satisfies all the properties
let rle_corrupted (inputStr:string) : (char*int) list =

  // helper
  let duplicateFirstTwoChars list =
    match list with
    | (ch1,n)::(ch2,m)::e3::e4::tail when n > 1 && m > 1 ->
      (ch1,1)::(ch2,1)::(ch1,n-1)::(ch2,m-1)::e3::e4::tail
    | _ ->
      list

  // start with correct output...
  let output = rle_recursive inputStr

  // ...and then corrupt it by
  // adding extra chars front and back
  output
  |> duplicateFirstTwoChars
  |> List.rev
  |> duplicateFirstTwoChars
  |> List.rev

Note that we only corrupt lists where:

• The run-lengths for the first two runs are > 1, so we can steal 1.
• There are at least four elements in the list, so that we can reverse and re-corrupt the other end. If you remove the match on ::e3::e4::, the implementation will fail the “reversed” property.

When we run our checker, then, we’ll want to increase the number of tests, because only a few of the inputs will meet the requirements for being corrupted and we want to make sure that we catch them.

Ok, let’s check this new EDFH implementation against the compound property propRle that we defined last time. As before, we will use a custom generator arbPixels to generate strings that have lots of runs in them.

let prop = Prop.forAll arbPixels (propRle rle_corrupted)

// check it thoroughly
let config = { Config.Default with MaxTest=10000}
Check.One(config,prop)
// Ok, passed 10000 tests.

And it passed. Oh dear! How are we going to defeat the EDFH now?

In an earlier post, I described a number of approaches that could be used to come up with properties. We already used one of them (“some things never change”) to require an invariant, namely that every character in the source string also occurs in the RLE. We will use two more of them in this post:

• “Different paths, same destination”
• “There and back again”

For our first approach, we will use a variant of the “commutative diagram” approach.

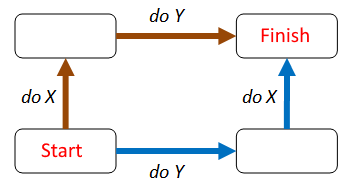
In this case we’re going exploit the fact that run-length encoding is a “structure-preserving” operation. What that means is that operations in “string world” are preserved after being transformed onto “RLE world”.

The defining operation on strings is concatenation (because strings are monoids) and so we require that a structure-preserving operation on strings maps concatenation in string world to concatenation in the target world

OP(str1 + str2) = OP(str1) + OP(str2)

An example of a simple structure-preserving operation on strings is strLen. It’s not just a random map from strings onto integers, because it preserves the concatenation operation.

strLen(str1 + str2) = strLen(str1) + strLen(str2)

It’s important to note that “structure-preserving” doesn’t mean that it preserves the content of the string, just that it preserves the relationships between strings. The strLen function above doesn’t preserve the content of the string, and you could even have a empty function that maps all strings onto an empty list. It doesn’t preserve the content, but it does preserve the structure, because:

empty(str1 + str2) = empty(str1) + empty(str2)

In our case, we want the rle function to preserve the structure of strings as well, which means that we need:

rle(str1 + str2) = rle(str1) + rle(str2)

So now all we need is a way to “add” two Rle structures. Even though they are lists, we can’t just concatenate them directly, because we may end up with adjacent runs. Instead, we want runs of the same character to be merged:

// wrong
['a',1] + ['a',1]  //=> [('a',1); ('a',1)]
// correct
['a',1] + ['a',1]  //=> [('a',2)]

Here’s the implementation of a function like that. It’s a bit tricky with all the special cases.

// A Rle is a list of chars and run-lengths
type Rle = (char*int) list

let rec rleConcat (rle1:Rle) (rle2:Rle) =
  match rle1 with
  // 0 elements, so return rle2
  | [] -> rle2

  // 1 element left, so compare with
  // first element of rle2 and merge if equal
  | [ (x,xCount) ] ->
    match rle2 with
    | [] ->
      rle1
    | (y,yCount)::tail ->
      if x = y then
        // merge
        (x,(xCount+yCount)) :: tail
      else
        (x,xCount)::(y,yCount)::tail

  // longer than 1, so recurse
  | head::tail ->
    head :: (rleConcat tail rle2)

Some interactive testing to make sure it looks good:

rleConcat ['a',1] ['a',1]  //=> [('a',2)]
rleConcat ['a',1] ['b',1]  //=> [('a',1); ('b',1)]

let rle1 = rle_recursive "aaabb"
let rle2 = rle_recursive "bccc"
let rle3 = rle_recursive ("aaabb" + "bccc")
rle3 = rleConcat rle1 rle2   //=> true

We’ve got our RLE “concat” function now, so we can define a property that checks that a RLE implementation preserves string concatenation.

let propConcat (impl:RleImpl) (str1,str2) =
  let ( <+> ) = rleConcat

  let rle1 = impl str1
  let rle2 = impl str2
  let actual = rle1 <+> rle2
  let expected = impl (str1 + str2)
  actual = expected

This property needs a pair of strings, not just one, so we need to create a new generator:

let arbPixelsPair =
  arbPixels.Generator
  |> Gen.two
  |> Arb.fromGen

Finally we can check the EDFH implementation against the property:

let prop = Prop.forAll arbPixelsPair (propConcat rle_corrupted)

// check it thoroughly
let config = { Config.Default with MaxTest=10000}
Check.One(config,prop)
// Falsifiable, after 2 tests

It fails! But the correct implementation still succeeds:

let prop = Prop.forAll arbPixelsPair (propConcat rle_recursive)

// check it thoroughly
let config = { Config.Default with MaxTest=10000}
Check.One(config,prop)
// Ok, passed 10000 tests.

Let’s review. We can replace the overly constrained “reverse” property with the more general “concat-preserving” property, so that our properties for a run-length encoding implementation are these:

• Content invariance: The output must contain all the characters from the input, in the same order.
• Runs are distinct: Two adjacent characters in the output cannot be the same.
• Same total length: The sum of the run lengths in the output must equal the total length of the input.
• Structure-preserving: Must preserve concatenation as above.

We have four separate properties, each of which has to be discovered and implemented separately. Is there an easier way? Yes there is!

If we go right back to the purpose of a run-length encoding, it is supposed to represent a string in a compressed but lossless way. “Lossless” is key. That means that we have a inverse function – a function that can recreate the original string from the RLE data structure.

Since we have an inverse, we can do a “there and back” test. An encoding followed by a decoding should take us back to where we started.

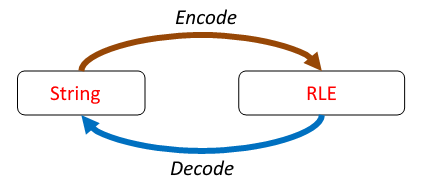
Before we start working on the decoder, let’s stop and define a proper type for a RLE encoding so that we can encapsulate it a bit. This will prove to be useful later.

type Rle = Rle of (char*int) list

We should now go back and change our earlier “encoding” implementations to return an Rle now. I’ll leave that as an exercise.

Implementing a decoder that accepts a Rle and returns a string is straightforward. There are lots of ways to do this. I’m choosing to use a mutable StringBuilder and nested loops for performance.

let decode (Rle rle) : string =
  let sb = System.Text.StringBuilder()
  for (ch,count) in rle do
    for _ in [1..count] do
      sb.Append(ch) |> ignore
  sb.ToString()

Let’s quickly test this interactively:

rle_recursive "111000011"
|> Rle     // wrap in Rle type
|> decode  //=> "111000011"

Ok, it seems to work. We could create a series of properties for testing decode separately from encoding, but we’ll just test them as a pair of inverses for now.

With the decode function available, we can write our “there and back again” property:

let propEncodeDecode (encode:RleImpl) inputStr =
  let actual =
    inputStr
    |> encode
    |> Rle  // wrap in Rle type
    |> decode

  actual = inputStr

Let’s check this property against the EDFH’s bad implementation, it fails. Excellent!

let prop = Prop.forAll arbPixels (propEncodeDecode rle_corrupted)

// check it thoroughly
let config = { Config.Default with MaxTest=10000}
Check.One(config,prop)
// Falsifiable, after 2 tests

And if we check this same property against our good implementation, it passes.

let prop = Prop.forAll arbPixels (propEncodeDecode rle_recursive)

// check it thoroughly
let config = { Config.Default with MaxTest=10000}
Check.One(config,prop)
// Ok, passed 10000 tests.

So we have finally created a property that beats the “corrupted” EDFH function.

However, we’re not done, because one of the previous EDFH implementations does satisfy this property, namely the very simplest one, rle_allChars.

/// a very simple RLE implementation
let rle_allChars inputStr =
  inputStr
  |> Seq.toList
  |> List.map (fun ch -> (ch,1))

// make a property 
let prop = Prop.forAll arbPixels (propEncodeDecode rle_allChars)

// and check it thoroughly
let config = { Config.Default with MaxTest=10000}
Check.One(config,prop)
// Ok, passed 10000 tests.

This is because it is a correct run-length encoding, just not a maximal one!

In the first post, I mentioned that I couldn’t quickly find a programmer-friendly specification for a RLE implementation. I think we have enough now.

First, RLE is lossless, so we can say that there must be an inverse function as well. Even without defining exactly what the inverse function is, we can say that the “round trip property” holds.

Second, we need to eliminate trivial encodings, such as the one where each run is of length one. We can do this by requiring runs to be maximal, which implies that adjacent runs do not share the same character.

And I think that is all we need. The other properties are implied. For example “contains all the characters from the input” is implied because of the round trip property. And the “sum of the run lengths” property is also implied for the same reason.

So, here’s the specification:

An RLE implementation is a pair of functions encode : string->Rle and decode : Rle->string, such that:

• Round trip. encode composed with decode is the same as the identity function.
• Maximal runs. No adjacent runs in the Rle structure share the same character, and all run-lengths are > 0.

Can you think of a way that the EDFH can break this specification? Let me know in the comments.

We could stop there, but let’s explore FsCheck some more.

Encoding and decoding are inverses of each other, so we could equally well define a property that started with decoding, and then encoded the result, like this:

let propDecodeEncode (encode:RleImpl) rle =
  let actual =
    rle
    |> decode
    |> encode
    |> Rle

  actual = rle

If we test this against the EDFH’s corrupting encoder, it fails:

let prop = propDecodeEncode rle_corrupted
Check.Quick(prop)
// Falsifiable, after 4 tests
// Rle [('a', 0)]

But it also it fails with our correct rle_recursive encoder.

let prop = propDecodeEncode rle_recursive
Check.Quick(prop)
// Falsifiable, after 4 tests
// Rle [('a', 0)]

Why is that? We can see immediately that FsCheck is generating a 0-length run, which when decoded and encoded, will give back an empty list. To fix this, we’ll have to create our own generator again.

Before we create a new generator though, let’s put some monitoring into place so that we can tell if it is actually working.

We’ll follow the same approach as before. First, we’ll define what “interesting” looks like and then we’ll create a dummy property to monitor the input.

First, we’ll say that an “interesting” RLE is one which is of non-trivial length and has some non-trivial runs in it.

let isInterestingRle (Rle rle) =
  let isLongList = rle.Length > 2
  let noOfLongRuns =
    rle
    |> List.filter (fun (_,run) -> run > 2)
    |> List.length
  isLongList && (noOfLongRuns > 2)

And then let’s use it to classify the inputs of a property:

let propIsInterestingRle input =
  let isInterestingInput = isInterestingRle input

  true // we don't care about the actual test
  |> Prop.classify (not isInterestingInput) "not interesting"
  |> Prop.classify isInterestingInput "interesting"

The result is clear – most of the inputs generated automatically by FsCheck are uninteresting.

Check.Quick propIsInterestingRle
// Ok, passed 100 tests.
// 99% not interesting.
// 1% interesting.

So let’s build a generator. We’ll pick a random character, and a random run-length, and combine them into a list of pairs, like this:

let arbRle =
  let genChar = Gen.elements ['a'..'z']
  let genRunLength = Gen.choose(1,10)
  Gen.zip genChar genRunLength
  |> Gen.listOf
  |> Gen.map Rle
  |> Arb.fromGen

If we check the property using this new generator the results are much better now:

let prop = Prop.forAll arbRle propIsInterestingRle
Check.Quick prop
// Ok, passed 100 tests.
// 86% interesting.
// 14% not interesting.

Let’s retest our correct implementation with this new generator.

let prop = Prop.forAll arbRle (propDecodeEncode rle_recursive)

// check it thoroughly
let config = { Config.Default with MaxTest=10000}
Check.One(config,prop)
// Falsifiable, after 82 tests
// Rle [('e', 7); ('e', 6); ('z', 10)]

Oops, we did it again. It still fails.

Fortunately, the counter-example shows us why. Two adjacent characters are the same, which means that the re-encoding won’t match up with the original one. The fix for this is to filter out these shared-character runs in the generator logic.

Here’s the code to remove adjacent runs:

let removeAdjacentRuns runList =
  let folder prevRuns run =
    match prevRuns with
    | [] -> [run]
    | head::_ ->
      if fst head <> fst run then
        // add
        run::prevRuns
      else
        // duplicate -- ignore
        prevRuns
  runList
  |> List.fold folder []
  |> List.rev

And here’s the updated generator:

let arbRle =
  let genChar = Gen.elements ['a'..'z']
  let genRunLength = Gen.choose(1,10)
  Gen.zip genChar genRunLength
  |> Gen.listOf
  |> Gen.map removeAdjacentRuns
  |> Gen.map Rle
  |> Arb.fromGen

And now, if we test one more time, everything works.

let prop = Prop.forAll arbRle (propDecodeEncode rle_recursive)

// check it thoroughly
let config = { Config.Default with MaxTest=10000}
Check.One(config,prop)
// Ok, passed 10000 tests.

FsCheck defines default generators for all the common types (string, int, etc.) and can also generate data for compound types (records, discriminated unions) by reflection, but as we have seen, we often need to have more control than this.

So far, we have been explicitly passing the arbRle instance into each test using Prop.forAll. FsCheck supports registering an Arbitrary for a type so that you don’t have to pass it every time. For a common type that will see lots of reuse, this is very convenient.

FsCheck provides a number of useful built-in types with custom generators, such as PositiveInt, NonWhiteSpaceString, and so on (see more in the FsCheck namespace). How can we add our custom type to this list?

The FsCheck documentation explains how. You first define a class with a static method for each Arbitrary that you want to register:

type MyGenerators =
  static member Rle() = arbRle

  // static member MyCustomType() = arbMyCustomType

and then register that class with FsCheck:

Arb.register<MyGenerators>()

Once it is registered, you can get samples:

Arb.generate<Rle> |> Gen.sample 5 4
// [Rle [('c', 2); ('m', 8)];
//  Rle [];
//  Rle [('e', 7); ('c', 2); ('s', 1); ('m', 8)];
//  Rle [('t', 3); ('e', 7); ('c', 2)]]

and check properties without needing Prop.forAll any more.

let prop = propDecodeEncode rle_recursive

Check.Quick(prop)
// Ok, passed 100 tests.

That concludes this series. We started with a tweet about how to answer an interviewing question is a silly way and ended up taking a long detour into FsCheck, ensuring that we have “interesting” inputs, building our own generators, and experimenting with different ways of using properties to gain confidence in an implementation.

I hope this has given you some ideas that you can use for your own property-based testing. Have fun!

Source code used in this post is available here.