Part of the "Understanding Parser Combinators" series (link)

Building a useful set of parser combinators

15 or so combinators that can be combined to parse almost anything

11 Nov 2015 This post is over 3 years old

UPDATE: Slides and video from my talk on this topic

In this series, we are looking at how applicative parsers and parser combinators work.

In the first post, we created the foundations of a parsing library.
In this post, we’ll build out the library with many other useful combinators. The combinator names will be copied from those used by FParsec, so that you can easily migrate to it.

1. Transforming the contents of a parser with “map”

When parsing, we often want to match a particular string, such as a reserved word like “if” or “where”. A string is just a sequence of characters, so surely we could use the same technique that we used to define anyOf in the first post, but using andThen instead of orElse?

Here’s a (failed) attempt to create a pstring parser using that approach:

let pstring str =
  str
  |> Seq.map pchar // convert into parsers
  |> Seq.reduce andThen

This doesn’t work, because the output of andThen is different from the input (a tuple, not a char) and so the reduce approach fails.

In order to solve this, we’ll need to use a different technique.

To get started, let’s try just matching a string of a specific length. Say, for example, that we want to match a three digits in a row. Well, we can do that using andThen:

let parseDigit =
  anyOf ['0'..'9']

let parseThreeDigits =
  parseDigit .>>. parseDigit .>>. parseDigit

If we run it like this:

run parseThreeDigits "123A"

then we get the result:

Success ((('1', '2'), '3'), "A")

It does work, but the result contains a tuple inside a tuple (('1', '2'), '3') which is fugly and hard to use. It would be so much more convenient to just have a simple string ("123").

But in order to turn ('1', '2'), '3') into "123", we’ll need a function that can reach inside of the parser and transform the result using an arbitrary passed in function.

Of course, what we need is the functional programmer’s best friend, map.

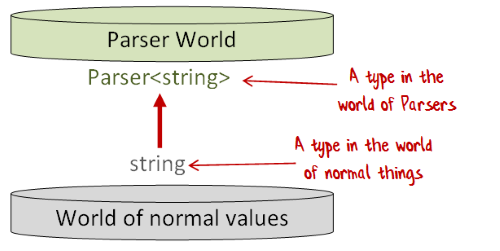
To understand map and similar functions, I like to think of there being two worlds: a “Normal World”, where regular things live, and “Parser World”, where Parsers live.

You can think of Parser World as a sort of “mirror” of Normal World because it obeys the following rules:

Every type in Normal World (say char) has a corresponding type in Parser World (Parser<char>).

And:

Every value in Normal World (say "ABC") has a corresponding value in Parser World (that is, some Parser<string> that returns "ABC").

And:

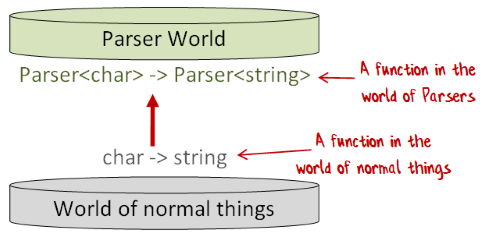
Every function in Normal World (say char -> string) has a corresponding function in Parser World (Parser<char> -> Parser<string>).

Using this metaphor then, map transforms (or “lifts”) a function in Normal World into a function in Parser World.

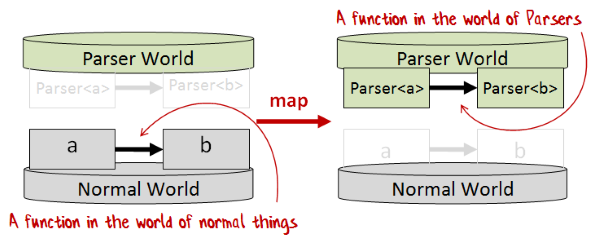
And by the way, if you like this metaphor, I have a whole series of posts that develop it further.

So that’s what map does; how do we implement it?

The logic is:

Inside the innerFn, run the parser to get the result.
If the result was a success, apply the specified function to the success value to get a new, transformed value, and…
…return the new, mapped, value instead of the original value.

Here’s the code (I’ve named the map function mapP to avoid confusion with other map functions):

let mapP f parser =
  let innerFn input =
    // run parser with the input
    let result = run parser input

    // test the result for Failure/Success
    match result with
    | Success (value,remaining) ->
      // if success, return the value transformed by f
      let newValue = f value
      Success (newValue, remaining)

    | Failure err ->
      // if failed, return the error
      Failure err
  // return the inner function
  Parser innerFn

If we look at the signature of mapP:

val mapP :
  f:('a -> 'b) -> Parser<'a> -> Parser<'b>

we can see that it has exactly the signature we want, transforming a function 'a -> 'b into a function Parser<'a> -> Parser<'b>.

It’s common to define an infix version of map as well:

let ( <!> ) = mapP

And in the context of parsing, we’ll often want to put the mapping function after the parser, with the parameters flipped. This makes using map with the pipeline idiom much more convenient:

let ( |>> ) x f = mapP f x

Parsing three digits with mapP

With mapP available, we can revisit parseThreeDigits and turn the tuple into a string.

Here’s the code:

let parseDigit = anyOf ['0'..'9']

let parseThreeDigitsAsStr =
  // create a parser that returns a tuple
  let tupleParser =
    parseDigit .>>. parseDigit .>>. parseDigit

  // create a function that turns the tuple into a string
  let transformTuple ((c1, c2), c3) =
    System.String [| c1; c2; c3 |]

  // use "map" to combine them
  mapP transformTuple tupleParser

Or, if you prefer a more compact implementation:

let parseThreeDigitsAsStr =
  (parseDigit .>>. parseDigit .>>. parseDigit)
  |>> fun ((c1, c2), c3) -> System.String [| c1; c2; c3 |]

And if we test it, we get a string in the result now, rather than a tuple:

run parseThreeDigitsAsStr "123A"  // Success ("123", "A")

We can go further, and map the string into an int:

let parseThreeDigitsAsInt =
  mapP int parseThreeDigitsAsStr

If we test this, we get an int in the Success branch.

run parseThreeDigitsAsInt "123A"  // Success (123, "A")

Let’s check the type of parseThreeDigitsAsInt:

val parseThreeDigitsAsInt : Parser<int>

It’s a Parser<int> now, not a Parser<char> or Parser<string>. The fact that a Parser can contain any type, not just a char or string, is a key feature that will be very valuable when we need to build more complex parsers.

2. Lifting functions to the world of Parsers

To achieve our goal of creating a parser that matches a list of characters, we need two more helper functions which I will call returnP and applyP.

returnP simply transforms a normal value into a value in Parser World
applyP transforms a Parser containing a function (Parser< 'a->'b >) into a function in Parser World (Parser<'a> -> Parser<'b >)

Here’s a diagram of returnP:

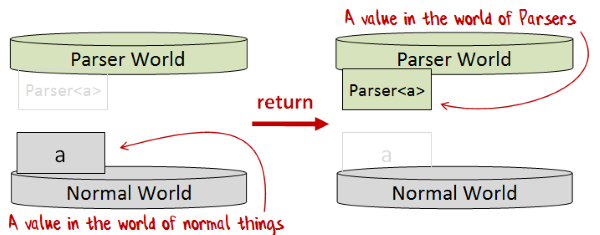
And here is the implementation of returnP:

let returnP x =
  let innerFn input =
    // ignore the input and return x
    Success (x,input )
  // return the inner function
  Parser innerFn

The signature of returnP is just as we want:

val returnP :
  'a -> Parser<'a>

Now here’s a diagram of applyP:

And here is the implementation of applyP, which uses .>>. and map:

let applyP fP xP =
  // create a Parser containing a pair (f,x)
  (fP .>>. xP)
  // map the pair by applying f to x
  |> mapP (fun (f,x) -> f x)

The infix version of applyP is written as <*>:

let ( <*> ) = applyP

Again, the signature of applyP is just as we want:

val applyP :
  Parser<('a -> 'b)> -> Parser<'a> -> Parser<'b>

Why do we need these two functions? Well, map will lift functions in Normal World into functions in Parser World, but only for one-parameter functions.

What’s great about returnP and applyP is that, together, they can lift any function in Normal World into a function in Parser World, no matter how many parameters it has.

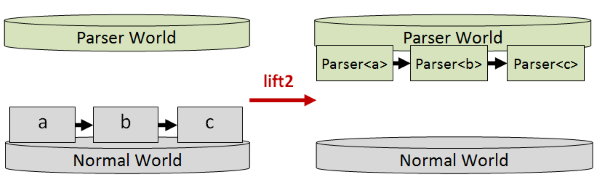
For example, we now can define a lift2 function that will lift a two parameter function into Parser World like this:

// lift a two parameter function to Parser World
let lift2 f xP yP =
  returnP f <*> xP <*> yP

The signature of lift2 is:

val lift2 :
  f:('a -> 'b -> 'c) -> Parser<'a> -> Parser<'b> -> Parser<'c>

Here’s a diagram of lift2:

If you want to know more about how this works, check out my “man page” post on lift2 or my explanation that involves the “Monadster”.

Let’s see some examples of using lift2 in practice. First, lifting integer addition to addition of Parsers:

let addP =
  lift2 (+)

The signature is:

val addP :
  Parser<int> -> Parser<int> -> Parser<int>

which shows that addP does indeed take two Parser<int> parameters and returns another Parser<int>.

And here’s the startsWith function being lifted to Parser World:

let startsWith (str:string) (prefix:string) =
  str.StartsWith(prefix)

let startsWithP =
  lift2 startsWith

Again, the signature of startsWithP is parallel to the signature of startsWith, but lifted to the world of Parsers.

val startsWith :
  str:string -> prefix:string -> bool

val startsWithP :
  Parser<string> -> Parser<string> -> Parser<bool>

3. Turning a list of Parsers into a single Parser

We now have the tools we need to implement our sequencing combinator! The logic will be:

Start with the list “cons” operator. This is the two-parameter function that prepends a “head” element onto a “tail” of elements to make a new list.
Lift cons into the world of Parsers using lift2.
We now have a a function that prepends a head Parser to a tail list of Parsers to make a new list of Parsers, where:
- The head Parser is the first element in the list of parsers that has been passed in.
- The tail is generated by calling the same function recursively with the next parser in the list.
When the input list is empty, just return a Parser containing an empty list.

Here’s the implementation:

let rec sequence parserList =
  // define the "cons" function, which is a two parameter function
  let cons head tail = head::tail

  // lift it to Parser World
  let consP = lift2 cons

  // process the list of parsers recursively
  match parserList with
  | [] ->
    returnP []
  | head::tail ->
    consP head (sequence tail)

The signature of sequence is:

val sequence :
  Parser<'a> list -> Parser<'a list>

which shows that the input is a list of Parsers and the output is a Parser containing a list of elements.

Let’s test it by creating a list of three parsers, and then combining them into one:

let parsers = [ pchar 'A'; pchar 'B'; pchar 'C' ]
let combined = sequence parsers

run combined "ABCD"
// Success (['A'; 'B'; 'C'], "D")

As you can see, when we run it we get back a list of characters, one for each parser in the original list.

Implementing the “pstring” parser

At last, we can implement the parser that matches a string, which we’ll call pstring.

The logic is:

Convert the string into a list of characters.
Convert each character into a Parser<char>.
Use sequence to convert the list of Parser<char> into a single Parser<char list>.
And finally, use map to convert the Parser<char list> into a Parser<string>.

Here’s the code:

/// Helper to create a string from a list of chars
let charListToStr charList =
    charList |> List.toArray |> System.String

// match a specific string
let pstring str =
  str
  // convert to list of char
  |> List.ofSeq
  // map each char to a pchar
  |> List.map pchar
  // convert to Parser<char list>
  |> sequence
  // convert Parser<char list> to Parser<string>
  |> mapP charListToStr

Let’s test it:

let parseABC = pstring "ABC"

run parseABC "ABCDE"  // Success ("ABC", "DE")
run parseABC "A|CDE"  // Failure "Expecting 'B'. Got '|'"
run parseABC "AB|DE"  // Failure "Expecting 'C'. Got '|'"

It works as expected. Phew!

4. Matching a parser multiple times

Another common need is to match a particular parser as many times as you can. For example:

When matching an integer, you want to match as many digit characters as you can.
When matching a run of whitespace, you want to match as many whitespace characters as you can.

There are slightly different requirements for these two cases.

When matching whitespace, it is often optional, so we want a “zero or more” matcher, which we’ll call many.
On the other hand, when matching digits for an integer, you want to match at least one digit, so we want a “one or more” matcher, which we’ll call many1.

Before creating these, we’ll define a helper function which matches a parser zero or more times. The logic is:

Run the parser.
If the parser returns Failure (and this is key) just return an empty list. That is, this function can never fail!
If the parser succeeds:
- Call the function recursively to get the remaining values (which could also be an empty list).
- Then combine the first value and the remaining values.

Here’s the code:

let rec parseZeroOrMore parser input =
  // run parser with the input
  let firstResult = run parser input
  // test the result for Failure/Success
  match firstResult with
  | Failure err ->
    // if parse fails, return empty list
    ([],input)
  | Success (firstValue,inputAfterFirstParse) ->
    // if parse succeeds, call recursively
    // to get the subsequent values
    let (subsequentValues,remainingInput) =
      parseZeroOrMore parser inputAfterFirstParse
    let values = firstValue::subsequentValues
    (values,remainingInput)

With this helper function, we can easily define many now – it’s just a wrapper over parseZeroOrMore:

/// match zero or more occurrences of the specified parser
let many parser =

  let innerFn input =
    // parse the input -- wrap in Success as it always succeeds
    Success (parseZeroOrMore parser input)

  Parser innerFn

The signature of many shows that the output is indeed a list of values wrapped in a Parser:

val many :
  Parser<'a> -> Parser<'a list>

Now let’s test many:

let manyA = many (pchar 'A')

// test some success cases
run manyA "ABCD"  // Success (['A'], "BCD")
run manyA "AACD"  // Success (['A'; 'A'], "CD")
run manyA "AAAD"  // Success (['A'; 'A'; 'A'], "D")

// test a case with no matches
run manyA "|BCD"  // Success ([], "|BCD")

Note that in the last case, even when there is nothing to match, the function succeeds.

There’s nothing about many that restricts its use to single characters. For example, we can use it to match repetitive string sequences too:

let manyAB = many (pstring "AB")

run manyAB "ABCD"  // Success (["AB"], "CD")
run manyAB "ABABCD"  // Success (["AB"; "AB"], "CD")
run manyAB "ZCD"  // Success ([], "ZCD")
run manyAB "AZCD"  // Success ([], "AZCD")

Finally, let’s implement the original example of matching whitespace:

let whitespaceChar = anyOf [' '; '\t'; '\n']
let whitespace = many whitespaceChar

run whitespace "ABC"  // Success ([], "ABC")
run whitespace " ABC"  // Success ([' '], "ABC")
run whitespace "\tABC"  // Success (['\t'], "ABC")

Defining “many1”

We can also define the “one or more” combinator many1, using the following logic:

Run the parser.
If it fails, return the failure.
If it succeeds:
- Call the helper function parseZeroOrMore to get the remaining values.
- Then combine the first value and the remaining values.

/// match one or more occurrences of the specified parser
let many1 parser =
  let innerFn input =
    // run parser with the input
    let firstResult = run parser input
    // test the result for Failure/Success
    match firstResult with
    | Failure err ->
      Failure err // failed
    | Success (firstValue,inputAfterFirstParse) ->
      // if first found, look for zeroOrMore now
      let (subsequentValues,remainingInput) =
        parseZeroOrMore parser inputAfterFirstParse
      let values = firstValue::subsequentValues
      Success (values,remainingInput)
  Parser innerFn

Again, the signature of many1 shows that the output is indeed a list of values wrapped in a Parser:

val many1 :
  Parser<'a> -> Parser<'a list>

Now let’s test many1:

// define parser for one digit
let digit = anyOf ['0'..'9']

// define parser for one or more digits
let digits = many1 digit

run digits "1ABC"  // Success (['1'], "ABC")
run digits "12BC"  // Success (['1'; '2'], "BC")
run digits "123C"  // Success (['1'; '2'; '3'], "C")
run digits "1234"  // Success (['1'; '2'; '3'; '4'], "")

run digits "ABC"   // Failure "Expecting '9'. Got 'A'"

As we saw in an earlier example, the last case gives a misleading error. It says “Expecting ‘9’” when it really should say “Expecting a digit”. In the next post we’ll fix this.

Parsing an integer

Using many1, we can create a parser for an integer. The implementation logic is:

Create a parser for a digit.
Use many1 to get a list of digits.
Using map, transform the result (a list of digits) into a string and then into an int.

Here’s the code:

let pint =
  // helper
  let resultToInt digitList =
    // ignore int overflow for now
    digitList |> List.toArray |> System.String |> int

  // define parser for one digit
  let digit = anyOf ['0'..'9']

  // define parser for one or more digits
  let digits = many1 digit

  // map the digits to an int
  digits
  |> mapP resultToInt

And let’s test it:

run pint "1ABC"  // Success (1, "ABC")
run pint "12BC"  // Success (12, "BC")
run pint "123C"  // Success (123, "C")
run pint "1234"  // Success (1234, "")

run pint "ABC"   // Failure "Expecting '9'. Got 'A'"

5. Matching a parser zero or one time

Sometimes we only want to match a parser zero or one time. For example, the pint parser above does not handle negative values. To correct this, we need to be able to handle an optional minus sign.

We can define an opt combinator easily:

Change the result of a specified parser to an option by mapping the result to Some.
Create another parser that always returns None.
Use <|> to choose the second (“None”) parser if the first fails.

Here’s the code:

let opt p =
  let some = p |>> Some
  let none = returnP None
  some <|> none

Here’s an example of it in use – we match a digit followed by an optional semicolon:

let digit = anyOf ['0'..'9']
let digitThenSemicolon = digit .>>. opt (pchar ';')

run digitThenSemicolon "1;"  // Success (('1', Some ';'), "")
run digitThenSemicolon "1"   // Success (('1', None), "")

And here is pint rewritten to handle an optional minus sign:

let pint =
  // helper
  let resultToInt (sign,charList) =
    let i = charList |> List.toArray |> System.String |> int
    match sign with
    | Some ch -> -i  // negate the int
    | None -> i

  // define parser for one digit
  let digit = anyOf ['0'..'9']

  // define parser for one or more digits
  let digits = many1 digit

  // parse and convert
  opt (pchar '-') .>>. digits
  |>> resultToInt

Note that the resultToInt helper function now needs to handle the sign option as well as the list of digits.

And here it is in action:

run pint "123C"   // Success (123, "C")
run pint "-123C"  // Success (-123, "C")

6. Throwing results away

We often want to match something in the input, but we don’t care about the parsed value itself. For example:

For a quoted string, we need to parse the quotes, but we don’t need the quotes themselves.
For a statement ending in a semicolon, we need to ensure the semicolon is there, but we don’t need the semicolon itself.
For whitespace separators, we need to ensure the whitespace is there, but we don’t need the actual whitespace data.

To handle these requirements, we will define some new combinators that throw away the results of a parser:

p1 >>. p2 will apply p1 and p2 in sequence, just like .>>., but throw away the result of p1 and keep the result of p2.
p1 .>> p2 will apply p1 and p2 in sequence, just like .>>., but keep the result of p1 and throw away the result of p2.

These are easy to define – just map over the result of .>>., which is a tuple, and keep only one element of the pair.

/// Keep only the result of the left side parser
let (.>>) p1 p2 =
  // create a pair
  p1 .>>. p2
  // then only keep the first value
  |> mapP (fun (a,b) -> a)

/// Keep only the result of the right side parser
let (>>.) p1 p2 =
  // create a pair
  p1 .>>. p2
  // then only keep the second value
  |> mapP (fun (a,b) -> b)

These combinators allow us to simplify the digitThenSemicolon example shown earlier:

let digit = anyOf ['0'..'9']

// use .>> below
let digitThenSemicolon = digit .>> opt (pchar ';')

run digitThenSemicolon "1;"  // Success ('1', "")
run digitThenSemicolon "1"   // Success ('1', "")

You can see that the result now is the same, whether or not the semicolon was present.

How about an example with whitespace?

The following code creates a parser that looks for “AB” followed by one or more whitespace chars, followed by “CD”.

let whitespaceChar = anyOf [' '; '\t'; '\n']
let whitespace = many1 whitespaceChar

let ab = pstring "AB"
let cd = pstring "CD"
let ab_cd = (ab .>> whitespace) .>>. cd

run ab_cd "AB \t\nCD"   // Success (("AB", "CD"), "")

The result contains “AB” and “CD” only. The whitespace between them has been discarded.

Introducing “between”

A particularly common requirement is to look for a parser between delimiters such as quotes or brackets.

Creating a combinator for this is trivial:

/// Keep only the result of the middle parser
let between p1 p2 p3 =
  p1 >>. p2 .>> p3

And here it is in use, to parse a quoted integer:

let pdoublequote = pchar '"'
let quotedInteger = between pdoublequote pint pdoublequote

run quotedInteger "\"1234\""   // Success (1234, "")
run quotedInteger "1234"       // Failure "Expecting '"'. Got '1'"

7. Parsing lists with separators

Another common requirement is parsing lists, separated by something like commas or whitespace.

To implement a “one or more” list, we need to:

First combine the separator and parser into one combined parser, but using >>. to throw away the separator value.
Next, look for a list of the separator/parser combo using many.
Then prefix that with the first parser and combine the results.

Here’s the code:

/// Parses one or more occurrences of p separated by sep
let sepBy1 p sep =
  let sepThenP = sep >>. p
  p .>>. many sepThenP
  |>> fun (p,pList) -> p::pList

For the “zero or more” version, we can choose the empty list as an alternate if sepBy1 does not find any matches:

/// Parses zero or more occurrences of p separated by sep
let sepBy p sep =
  sepBy1 p sep <|> returnP []

Here’s some tests for sepBy1 and sepBy, with results shown in the comments:

let comma = pchar ','
let digit = anyOf ['0'..'9']

let zeroOrMoreDigitList = sepBy digit comma
let oneOrMoreDigitList = sepBy1 digit comma

run oneOrMoreDigitList "1;"      // Success (['1'], ";")
run oneOrMoreDigitList "1,2;"    // Success (['1'; '2'], ";")
run oneOrMoreDigitList "1,2,3;"  // Success (['1'; '2'; '3'], ";")
run oneOrMoreDigitList "Z;"      // Failure "Expecting '9'. Got 'Z'"

run zeroOrMoreDigitList "1;"     // Success (['1'], ";")
run zeroOrMoreDigitList "1,2;"   // Success (['1'; '2'], ";")
run zeroOrMoreDigitList "1,2,3;" // Success (['1'; '2'; '3'], ";")
run zeroOrMoreDigitList "Z;"     // Success ([], "Z;")

What about “bind”?

One combinator that we haven’t implemented so far is bind (or >>=).

If you know anything about functional programming, or have seen my talk on FP patterns, you’ll know that bind is a powerful tool that can be used to implement many functions.

Up to this point, I thought that it would be better to show implementations for combinators such as map and .>>. that were explicit and thus, hopefully, easier to understand.

But now that we have some experience, let’s implement bind and see what we can do with it.

Here’s the implementation of bindP (as I’ll call it)

/// "bindP" takes a parser-producing function f, and a parser p
/// and passes the output of p into f, to create a new parser
let bindP f p =
  let innerFn input =
    let result1 = run p input
    match result1 with
    | Failure err ->
      // return error from parser1
      Failure err
    | Success (value1,remainingInput) ->
      // apply f to get a new parser
      let p2 = f value1
      // run parser with remaining input
      run p2 remainingInput
  Parser innerFn

The signature of bindP is:

val bindP :
  f:('a -> Parser<'b>) -> Parser<'a> -> Parser<'b>

which conforms to a standard bind signature. The input f is a “diagonal” function ('a -> Parser<'b>) and the output is a “horizontal” function (Parser<'a> -> Parser<'b>). See this post for more details on how bind works.

The infix version of bind is >>=. Note that the parameters are flipped: f is now the second parameter which makes it more convenient for F#’s pipeline idiom.

let ( >>= ) p f = bindP f p

Reimplementing other combinators using “bind”

The combination of bindP and returnP can be used to re-implement many of the other combinators. Here are some examples:

let mapP f =
  bindP (f >> returnP)

let andThen p1 p2 =
  p1 >>= (fun p1Result ->
  p2 >>= (fun p2Result ->
    returnP (p1Result,p2Result) ))

let applyP fP xP =
  fP >>= (fun f ->
  xP >>= (fun x ->
    returnP (f x) ))

// (assuming "many" is defined)

let many1 p =
  p      >>= (fun head ->
  many p >>= (fun tail ->
    returnP (head::tail) ))

Note that the combinators that check the Failure path can not be implemented using bind. These include orElse and many.

Review

We could keep building combinators for ever, but I think we have everything we need to build a JSON parser now, so let’s stop and review what we have done.

In the previous post we created these combinators:

.>>. (andThen) applies the two parsers in sequence and returns the results in a tuple.
<|> (orElse) applies the first parser, and if that fails, the second parsers.
choice extends orElse to choose from a list of parsers.

And in this post we created the following additional combinators:

bindP chains the result of a parser to another parser-producing function.
mapP transforms the result of a parser.
returnP lifts an normal value into the world of parsers.
applyP allows us to lift multi-parameter functions into functions that work on Parsers.
lift2 uses applyP to lift two-parameter functions into Parser World.
sequence converts a list of Parsers into a Parser containing a list.
many matches zero or more occurrences of the specified parser.
many1 matches one or more occurrences of the specified parser.
opt matches an optional occurrence of the specified parser.
.>> keeps only the result of the left side parser.
>>. keeps only the result of the right side parser.
between keeps only the result of the middle parser.
sepBy parses zero or more occurrences of a parser with a separator.
sepBy1 parses one or more occurrences of a parser with a separator.

I hope you can see why the concept of “combinators” is so powerful; given just a few basic functions, we have built up a library of useful functions quickly and concisely.

Listing of the parser library so far

Here’s the complete listing for the parsing library so far – it’s about 200 lines of code now!

Source code used in this post is available here.

open System

/// Type that represents Success/Failure in parsing
type ParseResult<'a> =
  | Success of 'a
  | Failure of string

/// Type that wraps a parsing function
type Parser<'T> = Parser of (string -> ParseResult<'T * string>)

/// Parse a single character
let pchar charToMatch =
  // define a nested inner function
  let innerFn str =
    if String.IsNullOrEmpty(str) then
      Failure "No more input"
    else
      let first = str.[0]
      if first = charToMatch then
        let remaining = str.[1..]
        Success (charToMatch,remaining)
      else
        let msg = sprintf "Expecting '%c'. Got '%c'" charToMatch first
        Failure msg
  // return the "wrapped" inner function
  Parser innerFn

/// Run a parser with some input
let run parser input =
  // unwrap parser to get inner function
  let (Parser innerFn) = parser
  // call inner function with input
  innerFn input

/// "bindP" takes a parser-producing function f, and a parser p
/// and passes the output of p into f, to create a new parser
let bindP f p =
  let innerFn input =
    let result1 = run p input
    match result1 with
    | Failure err ->
      // return error from parser1
      Failure err
    | Success (value1,remainingInput) ->
      // apply f to get a new parser
      let p2 = f value1
      // run parser with remaining input
      run p2 remainingInput
  Parser innerFn

/// Infix version of bindP
let ( >>= ) p f = bindP f p

/// Lift a value to a Parser
let returnP x =
  let innerFn input =
    // ignore the input and return x
    Success (x,input)
  // return the inner function
  Parser innerFn

/// apply a function to the value inside a parser
let mapP f =
  bindP (f >> returnP)

/// infix version of mapP
let ( <!> ) = mapP

/// "piping" version of mapP
let ( |>> ) x f = mapP f x

/// apply a wrapped function to a wrapped value
let applyP fP xP =
  fP >>= (fun f ->
  xP >>= (fun x ->
    returnP (f x) ))

/// infix version of apply
let ( <*> ) = applyP

/// lift a two parameter function to Parser World
let lift2 f xP yP =
  returnP f <*> xP <*> yP

/// Combine two parsers as "A andThen B"
let andThen p1 p2 =
  p1 >>= (fun p1Result ->
  p2 >>= (fun p2Result ->
    returnP (p1Result,p2Result) ))

/// Infix version of andThen
let ( .>>. ) = andThen

/// Combine two parsers as "A orElse B"
let orElse p1 p2 =
  let innerFn input =
    // run parser1 with the input
    let result1 = run p1 input

    // test the result for Failure/Success
    match result1 with
    | Success result ->
      // if success, return the original result
      result1

    | Failure err ->
      // if failed, run parser2 with the input
      let result2 = run p2 input

      // return parser2's result
      result2

  // return the inner function
  Parser innerFn

/// Infix version of orElse
let ( <|> ) = orElse

/// Choose any of a list of parsers
let choice listOfParsers =
  List.reduce ( <|> ) listOfParsers

/// Choose any of a list of characters
let anyOf listOfChars =
  listOfChars
  |> List.map pchar // convert into parsers
  |> choice

/// Convert a list of Parsers into a Parser of a list
let rec sequence parserList =
  // define the "cons" function, which is a two parameter function
  let cons head tail = head::tail

  // lift it to Parser World
  let consP = lift2 cons

  // process the list of parsers recursively
  match parserList with
  | [] ->
    returnP []
  | head::tail ->
    consP head (sequence tail)

/// (helper) match zero or more occurrences of the specified parser
let rec parseZeroOrMore parser input =
  // run parser with the input
  let firstResult = run parser input
  // test the result for Failure/Success
  match firstResult with
  | Failure err ->
    // if parse fails, return empty list
    ([],input)
  | Success (firstValue,inputAfterFirstParse) ->
    // if parse succeeds, call recursively
    // to get the subsequent values
    let (subsequentValues,remainingInput) =
      parseZeroOrMore parser inputAfterFirstParse
    let values = firstValue::subsequentValues
    (values,remainingInput)

/// matches zero or more occurrences of the specified parser
let many parser =
  let innerFn input =
    // parse the input -- wrap in Success as it always succeeds
    Success (parseZeroOrMore parser input)

  Parser innerFn

/// matches one or more occurrences of the specified parser
let many1 p =
  p      >>= (fun head ->
  many p >>= (fun tail ->
    returnP (head::tail) ))

/// Parses an optional occurrence of p and returns an option value.
let opt p =
  let some = p |>> Some
  let none = returnP None
  some <|> none

/// Keep only the result of the left side parser
let (.>>) p1 p2 =
  // create a pair
  p1 .>>. p2
  // then only keep the first value
  |> mapP (fun (a,b) -> a)

/// Keep only the result of the right side parser
let (>>.) p1 p2 =
  // create a pair
  p1 .>>. p2
  // then only keep the second value
  |> mapP (fun (a,b) -> b)

/// Keep only the result of the middle parser
let between p1 p2 p3 =
  p1 >>. p2 .>> p3

/// Parses one or more occurrences of p separated by sep
let sepBy1 p sep =
  let sepThenP = sep >>. p
  p .>>. many sepThenP
  |>> fun (p,pList) -> p::pList

/// Parses zero or more occurrences of p separated by sep
let sepBy p sep =
  sepBy1 p sep <|> returnP []

Summary

In this post, we have built on the basic parsing code from last time to create a library of a 15 or so combinators that can be combined to parse almost anything.

Soon, we’ll use them to build a JSON parser, but before that, let’s pause and take time to clean up the error messages. That will be the topic of the next post.

Source code used in this post is available here.

The "Understanding Parser Combinators" series

Understanding Parser Combinators
Building a parser combinator library from scratch
Building a useful set of parser combinators
15 or so combinators that can be combined to parse almost anything
Improving the parser library
Adding more informative errors
Writing a JSON parser from scratch
In 250 lines of code

Written by ScottW. Found a typo or error? Follow me on

Twitter.

1. Transforming the contents of a parser with “map”

Parsing three digits with mapP

2. Lifting functions to the world of Parsers

3. Turning a list of Parsers into a single Parser

Implementing the “pstring” parser

4. Matching a parser multiple times

Defining “many1”

Parsing an integer

5. Matching a parser zero or one time

6. Throwing results away

Introducing “between”

7. Parsing lists with separators

What about “bind”?

Reimplementing other combinators using “bind”

Review

Listing of the parser library so far

Summary

The "Understanding Parser Combinators" series

Comments