Worked example: A stack based calculator

In this post, we’ll implement a simple stack based calculator (also known as “reverse Polish” style). The implementation is almost entirely done with functions, with only one special type and no pattern matching at all, so it is a great testing ground for the concepts introduced in this series.

If you are not familiar with a stack based calculator, it works as follows: numbers are pushed on a stack, and operations such as addition and multiplication pop numbers off the stack and push the result back on.

Here is a diagram showing a simple calculation using a stack:

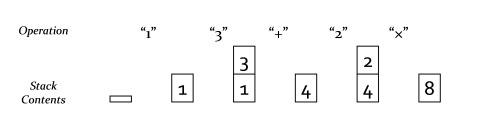
The first steps to designing a system like this is to think about how it would be used. Following a Forth like syntax, we will give each action a label, so that the example above might want to be written something like:

EMPTY ONE THREE ADD TWO MUL SHOW

We might not be able to get this exact syntax, but let’s see how close we can get.

First we need to define the data structure for a stack. To keep things simple, we’ll just use a list of floats.

type Stack = float list

But, hold on, let’s wrap it in a single case union type to make it more descriptive, like this:

type Stack = StackContents of float list

For more details on why this is nicer, read the discussion of single case union types in this post.

Now, to create a new stack, we use StackContents as a constructor:

let newStack = StackContents [1.0;2.0;3.0]

And to extract the contents of an existing Stack, we pattern match with StackContents:

let (StackContents contents) = newStack

// "contents" value set to
// float list = [1.0; 2.0; 3.0]

Next we need a way to push numbers on to the stack. This will be simply be prepending the new value at the front of the list using the “::” operator.

Here is our push function:

let push x aStack =
    let (StackContents contents) = aStack
    let newContents = x::contents
    StackContents newContents

This basic function has a number of things worth discussing.

First, note that the list structure is immutable, so the function must accept an existing stack and return a new stack. It cannot just alter the existing stack. In fact, all of the functions in this example will have a similar format like this:

Input: a Stack plus other parameters
Output: a new Stack

Next, what should the order of the parameters be? Should the stack parameter come first or last? If you remember the discussion of designing functions for partial application, you will remember that the most changeable thing should come last. You’ll see shortly that this guideline will be born out.

Finally, the function can be made more concise by using pattern matching in the function parameter itself, rather than using a let in the body of the function.

Here is the rewritten version:

let push x (StackContents contents) =
    StackContents (x::contents)

Much nicer!

And by the way, look at the nice signature it has:

val push : float -> Stack -> Stack

As we know from a previous post, the signature tells you a lot about the function. In this case, I could probably guess what it did from the signature alone, even without knowing that the name of the function was “push”. This is one of the reasons why it is a good idea to have explicit type names. If the stack type had just been a list of floats, it wouldn’t have been as self-documenting.

Anyway, now let’s test it:

let emptyStack = StackContents []
let stackWith1 = push 1.0 emptyStack
let stackWith2 = push 2.0 stackWith1

Works great!

With this simple function in place, we can easily define an operation that pushes a particular number onto the stack.

let ONE stack = push 1.0 stack
let TWO stack = push 2.0 stack

But wait a minute! Can you see that the stack parameter is used on both sides? In fact, we don’t need to mention it at all. Instead we can skip the stack parameter and write the functions using partial application as follows:

let ONE = push 1.0
let TWO = push 2.0
let THREE = push 3.0
let FOUR = push 4.0
let FIVE = push 5.0

Now you can see that if the parameters for push were in a different order, we wouldn’t have been able to do this.

While we’re at it, let’s define a function that creates an empty stack as well:

let EMPTY = StackContents []

Let’s test all of these now:

let stackWith1 = ONE EMPTY
let stackWith2 = TWO stackWith1
let stackWith3  = THREE stackWith2

These intermediate stacks are annoying – can we get rid of them? Yes! Note that these functions ONE, TWO, THREE all have the same signature:

Stack -> Stack

This means that they can be chained together nicely! The output of one can be fed into the input of the next, as shown below:

let result123 = EMPTY |> ONE |> TWO |> THREE
let result312 = EMPTY |> THREE |> ONE |> TWO

That takes care of pushing onto the stack – what about a pop function next?

When we pop the stack, we will return the top of the stack, obviously, but is that all?

In an object-oriented style, the answer is yes. In an OO approach, we would mutate the stack itself behind the scenes, so that the top element was removed.

But in a functional style, the stack is immutable. The only way to remove the top element is to create a new stack with the element removed. In order for the caller to have access to this new diminished stack, it needs to be returned along with the top element itself.

In other words, the pop function will have to return two values, the top plus the new stack. The easiest way to do this in F# is just to use a tuple.

Here’s the implementation:

/// Pop a value from the stack and return it
/// and the new stack as a tuple
let pop (StackContents contents) =
    match contents with
    | top::rest ->
        let newStack = StackContents rest
        (top,newStack)

This function is also very straightforward.

As before, we are extracting the contents directly in the parameter.

We then use a match..with expression to test the contents.

Next, we separate the top element from the rest, create a new stack from the remaining elements and finally return the pair as a tuple.

Try the code above and see what happens. You will get a compiler error! The compiler has caught a case we have overlooked – what happens if the stack is empty?

So now we have to decide how to handle this.

• Option 1: Return a special “Success” or “Error” state, as we did in a post from the “why use F#?” series.
• Option 2: Throw an exception.

Generally, I prefer to use error cases, but in this case, we’ll use an exception. So here’s the pop code changed to handle the empty case:

/// Pop a value from the stack and return it
/// and the new stack as a tuple
let pop (StackContents contents) =
    match contents with
    | top::rest ->
        let newStack = StackContents rest
        (top,newStack)
    | [] ->
        failwith "Stack underflow"

Now let’s test it:

let initialStack = EMPTY  |> ONE |> TWO
let popped1, poppedStack = pop initialStack
let popped2, poppedStack2 = pop poppedStack

and to test the underflow:

let _ = pop EMPTY

Now with both push and pop in place, we can work on the “add” and “multiply” functions:

let ADD stack =
   let x,s = pop stack  //pop the top of the stack
   let y,s2 = pop s     //pop the result stack
   let result = x + y   //do the math
   push result s2       //push back on the doubly-popped stack

let MUL stack =
   let x,s = pop stack  //pop the top of the stack
   let y,s2 = pop s     //pop the result stack
   let result = x * y   //do the math
   push result s2       //push back on the doubly-popped stack

Test these interactively:

let add1and2 = EMPTY |> ONE |> TWO |> ADD
let add2and3 = EMPTY |> TWO |> THREE |> ADD
let mult2and3 = EMPTY |> TWO |> THREE |> MUL

It works!

It is obvious that there is significant duplicate code between these two functions. How can we refactor?

Both functions pop two values from the stack, apply some sort of binary function, and then push the result back on the stack. This leads us to refactor out the common code into a “binary” function that takes a two parameter math function as a parameter:

let binary mathFn stack =
    // pop the top of the stack
    let y,stack' = pop stack
    // pop the top of the stack again
    let x,stack'' = pop stack'
    // do the math
    let z = mathFn x y
    // push the result value back on the doubly-popped stack
    push z stack''

Note that in this implementation, I’ve switched to using ticks to represent changed states of the “same” object, rather than numeric suffixes. Numeric suffixes can easily get quite confusing.

Question: why are the parameters in the order they are, instead of mathFn being after stack?

Now that we have binary, we can define ADD and friends more simply:

Here’s a first attempt at ADD using the new binary helper:

let ADD aStack = binary (fun x y -> x + y) aStack

But we can eliminate the lambda, as it is exactly the definition of the built-in + function! Which gives us:

let ADD aStack = binary (+) aStack

And again, we can use partial application to hide the stack parameter. Here’s the final definition:

let ADD = binary (+)

And here’s the definition of some other math functions:

let SUB = binary (-)
let MUL = binary (*)
let DIV = binary (/)

Let’s test interactively again.

let threeDivTwo = EMPTY |> THREE |> TWO |> DIV   // Answer: 1.5
let twoSubtractFive = EMPTY |> TWO |> FIVE |> SUB  // Answer: -3.0
let oneAddTwoSubThree = EMPTY |> ONE |> TWO |> ADD |> THREE |> SUB // Answer: 0.0

In a similar fashion, we can create a helper function for unary functions

let unary f stack =
    let x,stack' = pop stack  //pop the top of the stack
    push (f x) stack'         //push the function value on the stack

And then define some unary functions:

let NEG = unary (fun x -> -x)
let SQUARE = unary (fun x -> x * x)

Test interactively again:

let neg3 = EMPTY |> THREE |> NEG
let square2 = EMPTY |> TWO |> SQUARE

In the original requirements, we mentioned that we wanted to be able to show the results, so let’s define a SHOW function.

let SHOW stack =
    let x,_ = pop stack
    printfn "The answer is %f" x
    stack  // keep going with same stack

Note that in this case, we pop the original stack but ignore the diminished version. The final result of the function is the original stack, as if it had never been popped.

So now finally, we can write the code example from the original requirements

EMPTY |> ONE |> THREE |> ADD |> TWO |> MUL |> SHOW // (1+3)*2 = 8

This is fun – what else can we do?

Well, we can define a few more core helper functions:

/// Duplicate the top value on the stack
let DUP stack =
    // get the top of the stack
    let x,_ = pop stack
    // push it onto the stack again
    push x stack

/// Swap the top two values
let SWAP stack =
    let x,s = pop stack
    let y,s' = pop s
    push y (push x s')

/// Make an obvious starting point
let START  = EMPTY

And with these additional functions in place, we can write some nice examples:

START
    |> ONE |> TWO |> SHOW

START
    |> ONE |> TWO |> ADD |> SHOW
    |> THREE |> ADD |> SHOW

START
    |> THREE |> DUP |> DUP |> MUL |> MUL // 27

START
    |> ONE |> TWO |> ADD |> SHOW  // 3
    |> THREE |> MUL |> SHOW       // 9
    |> TWO |> DIV |> SHOW         // 9 div 2 = 4.5

But that’s not all. In fact, there is another very interesting way to think about these functions.

As I pointed out earlier, they all have an identical signature:

Stack -> Stack

So, because the input and output types are the same, these functions can be composed using the composition operator >>, not just chained together with pipes.

Here are some examples:

// define a new function
let ONE_TWO_ADD =
    ONE >> TWO >> ADD

// test it
START |> ONE_TWO_ADD |> SHOW

// define a new function
let SQUARE =
    DUP >> MUL

// test it
START |> TWO |> SQUARE |> SHOW

// define a new function
let CUBE =
    DUP >> DUP >> MUL >> MUL

// test it
START |> THREE |> CUBE |> SHOW

// define a new function
let SUM_NUMBERS_UPTO =
    DUP      // n, n           2 items on stack
    >> ONE   // n, n, 1        3 items on stack
    >> ADD   // n, (n+1)       2 items on stack
    >> MUL   // n(n+1)         1 item on stack
    >> TWO   // n(n+1), 2      2 items on stack
    >> DIV   // n(n+1)/2       1 item on stack

// test it with sum of numbers up to 9
START |> THREE |> SQUARE |> SUM_NUMBERS_UPTO |> SHOW  // 45

In each of these cases, a new function is defined by composing other functions together to make a new one. This is a good example of the “combinator” approach to building up functionality.

We have now seen two different ways that this stack based model can be used; by piping or by composition. So what is the difference? And why would we prefer one way over another?

The difference is that piping is, in a sense, a “realtime transformation” operation. When you use piping you are actually doing the operations right now, passing a particular stack around.

On the other hand, composition is a kind of “plan” for what you want to do, building an overall function from a set of parts, but not actually running it yet.

So for example, I can create a “plan” for how to square a number by combining smaller operations:

let COMPOSED_SQUARE = DUP >> MUL

I cannot do the equivalent with the piping approach.

let PIPED_SQUARE = DUP |> MUL

This causes a compilation error. I have to have some sort of concrete stack instance to make it work:

let stackWith2 = EMPTY |> TWO
let twoSquared = stackWith2 |> DUP |> MUL

And even then, I only get the answer for this particular input, not a plan for all possible inputs, as in the COMPOSED_SQUARE example.

The other way to create a “plan” is to explicitly pass in a lambda to a more primitive function, as we saw near the beginning:

let LAMBDA_SQUARE = unary (fun x -> x * x)

This is much more explicit (and is likely to be faster) but loses all the benefits and clarity of the composition approach.

So, in general, go for the composition approach if you can!

Here’s the complete code for all the examples so far.

// ==============================================
// Types
// ==============================================

type Stack = StackContents of float list

// ==============================================
// Stack primitives
// ==============================================

/// Push a value on the stack
let push x (StackContents contents) =
    StackContents (x::contents)

/// Pop a value from the stack and return it
/// and the new stack as a tuple
let pop (StackContents contents) =
    match contents with
    | top::rest ->
        let newStack = StackContents rest
        (top,newStack)
    | [] ->
        failwith "Stack underflow"

// ==============================================
// Operator core
// ==============================================

// pop the top two elements
// do a binary operation on them
// push the result
let binary mathFn stack =
    let y,stack' = pop stack
    let x,stack'' = pop stack'
    let z = mathFn x y
    push z stack''

// pop the top element
// do a unary operation on it
// push the result
let unary f stack =
    let x,stack' = pop stack
    push (f x) stack'

// ==============================================
// Other core
// ==============================================

/// Pop and show the top value on the stack
let SHOW stack =
    let x,_ = pop stack
    printfn "The answer is %f" x
    stack  // keep going with same stack

/// Duplicate the top value on the stack
let DUP stack =
    let x,s = pop stack
    push x (push x s)

/// Swap the top two values
let SWAP stack =
    let x,s = pop stack
    let y,s' = pop s
    push y (push x s')

/// Drop the top value on the stack
let DROP stack =
    let _,s = pop stack  //pop the top of the stack
    s                    //return the rest

// ==============================================
// Words based on primitives
// ==============================================

// Constants
// -------------------------------
let EMPTY = StackContents []
let START  = EMPTY


// Numbers
// -------------------------------
let ONE = push 1.0
let TWO = push 2.0
let THREE = push 3.0
let FOUR = push 4.0
let FIVE = push 5.0

// Math functions
// -------------------------------
let ADD = binary (+)
let SUB = binary (-)
let MUL = binary (*)
let DIV = binary (/)

let NEG = unary (fun x -> -x)


// ==============================================
// Words based on composition
// ==============================================

let SQUARE =
    DUP >> MUL

let CUBE =
    DUP >> DUP >> MUL >> MUL

let SUM_NUMBERS_UPTO =
    DUP      // n, n           2 items on stack
    >> ONE   // n, n, 1        3 items on stack
    >> ADD   // n, (n+1)       2 items on stack
    >> MUL   // n(n+1)         1 item on stack
    >> TWO   // n(n+1), 2      2 items on stack
    >> DIV   // n(n+1)/2       1 item on stack

So there we have it, a simple stack based calculator. We’ve seen how we can start with a few primitive operations (push, pop, binary, unary) and from them, build up a whole domain specific language that is both easy to implement and easy to use.

As you might guess, this example is based heavily on the Forth language. I highly recommend the free book “Thinking Forth”, which is not just about the Forth language, but about (non object-oriented!) problem decomposition techniques which are equally applicable to functional programming.

I got the idea for this post from a great blog by Ashley Feniello. If you want to go deeper into emulating a stack based language in F#, start there. Have fun!