Understanding bind

This post is the second in a series. In the previous post, I described some of the core functions for lifting a value from a normal world to an elevated world.

In this post, we’ll look at “world-crossing” functions, and how they can be tamed with the bind function.

Here’s a list of shortcuts to the various functions mentioned in this series:

• Part 1: Lifting to the elevated world
  • The map function
  • The return function
  • The apply function
  • The liftN family of functions
  • The zip function and ZipList world
• Part 2: How to compose world-crossing functions
  • The bind function
  • List is not a monad. Option is not a monad.
• Part 3: Using the core functions in practice
  • Independent and dependent data
  • Example: Validation using applicative style and monadic style
  • Lifting to a consistent world
  • Kleisli world
• Part 4: Mixing lists and elevated values
  • Mixing lists and elevated values
  • The traverse/MapM function
  • The sequence function
  • “Sequence” as a recipe for ad-hoc implementations
  • Readability vs. performance
  • Dude, where’s my filter?
• Part 5: A real-world example that uses all the techniques
  • Example: Downloading and processing a list of websites
  • Treating two worlds as one
• Part 6: Designing your own elevated world
  • Designing your own elevated world
  • Filtering out failures
  • The Reader monad
• Part 7: Summary
  • List of operators mentioned
  • Further reading

Common Names: bind, flatMap, andThen, collect, SelectMany

Common Operators: >>= (left to right), =<< (right to left )

What it does: Allows you to compose world-crossing (“monadic”) functions

Signature: (a->E<b>) -> E<a> -> E<b>. Alternatively with the parameters reversed: E<a> -> (a->E<b>) -> E<b>

We frequently have to deal with functions that cross between the normal world and the elevated world.

For example: a function that parses a string to an int might return an Option<int> rather than a normal int, a function that reads lines from a file might return IEnumerable<string>, a function that fetches a web page might return Async<string>, and so on.

These kinds of “world-crossing” functions are recognizable by their signature a -> E<b>; their input is in the normal world but their output is in the elevated world. Unfortunately, this means that these kinds of functions cannot be linked together using standard composition.

What “bind” does is transform a world-crossing function (commonly known as a “monadic function”) into a lifted function E<a> -> E<b>.

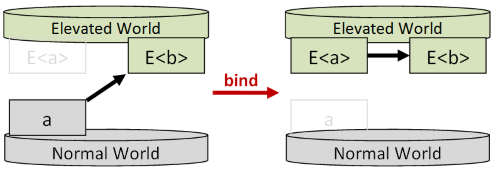
The benefit of doing this is that the resulting lifted functions live purely in the elevated world, and so can be combined easily by composition.

For example, a function of type a -> E<b> cannot be directly composed with a function of type b -> E<c>, but after bind is used, the second function becomes of type E<b> -> E<c>, which can be composed.

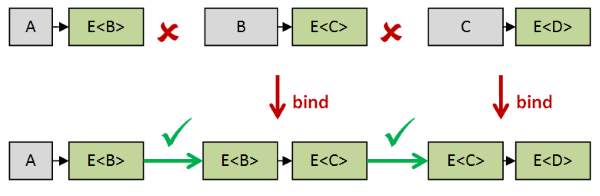
In this way, bind lets us chain together any number of monadic functions.

An alternative interpretation of bind is that it is a two parameter function that takes a elevated value (E<a>) and a “monadic function” (a -> E<b>), and returns a new elevated value (E<b>) generated by “unwrapping” the value inside the input, and running the function a -> E<b> against it. Of course, the “unwrapping” metaphor does not work for every elevated world, but still it can often be useful to think of it this way.

Here are some examples of defining bind for two different types in F#:

module Option =

    // The bind function for Options
    let bind f xOpt =
        match xOpt with
        | Some x -> f x
        | _ -> None
    // has type : ('a -> 'b option) -> 'a option -> 'b option

module List =

    // The bind function for lists
    let bindList (f: 'a->'b list) (xList: 'a list)  =
        [ for x in xList do
          for y in f x do
              yield y ]
    // has type : ('a -> 'b list) -> 'a list -> 'b list

Notes:

• Of course, in these two particular cases, the functions already exist in F#, called Option.bind and List.collect.
• For List.bind I’m cheating again and using for..in..do, but I think that this particular implementation shows clearly how bind works with lists. There is a purer recursive implementation, but I won’t show that here.

As explained at the beginning of this section, bind can be used to compose cross-world functions. Let’s see how this works in practice with a simple example.

First let’s say we have a function that parses certain strings into ints. Here’s a very simple implementation:

let parseInt str =
    match str with
    | "-1" -> Some -1
    | "0" -> Some 0
    | "1" -> Some 1
    | "2" -> Some 2
    // etc
    | _ -> None

// signature is string -> int option

Sometimes it returns a int, sometimes not. So the signature is string -> int option – a cross-world function.

And let’s say we have another function that takes an int as input and returns a OrderQty type:

type OrderQty = OrderQty of int

let toOrderQty qty =
    if qty >= 1 then
        Some (OrderQty qty)
    else
        // only positive numbers allowed
        None

// signature is int -> OrderQty option

Again, it might not return an OrderQty if the input is not positive. The signature is therefore int -> OrderQty option – another cross-world function.

Now, how can we create a function that starts with an string and returns an OrderQty in one step?

The output of parseInt cannot be fed directly into toOrderQty, so this is where bind comes to the rescue!

Doing Option.bind toOrderQty lifts it to a int option -> OrderQty option function and so the output of parseInt can be used as input, just as we need.

let parseOrderQty str =
    parseInt str
    |> Option.bind toOrderQty
// signature is string -> OrderQty option

The signature of our new parseOrderQty is string -> OrderQty option, yet another cross-world function. So if we want to do something with the OrderQty that is output we may well have to use bind again on the next function in the chain.

As with apply, using the named bind function can be awkward, so it is common to create an infix version, typically called >>= (for left to right data flow) or =<< (for right to left data flow) .

With this in place you can write an alternative version of parseOrderQty like this:

let parseOrderQty_alt str =
    str |> parseInt >>= toOrderQty

You can see that >>= performs the same kind of role as pipe (|>) does, except that it works to pipe “elevated” values into cross-world functions.

Bind can be used to chain any number of functions or expressions together, so you often see code looking something like this:

expression1 >>=
expression2 >>=
expression3 >>=
expression4

This is not too different from how an imperative program might look if you replace the >>= with a ;:

statement1;
statement2;
statement3;
statement4;

Because of this, bind is sometimes called a “programmable semicolon”.

Most functional programming languages have some kind of syntax support for bind that lets you avoid having to write a series of continuations or use explicit binds.

In F# it is (one component of) computation expressions, so the following explicit chaining of bind:

initialExpression >>= (fun x ->
expressionUsingX  >>= (fun y ->
expressionUsingY  >>= (fun z ->
x+y+z )))             // return

becomes implicit, using let! syntax:

elevated {
    let! x = initialExpression
    let! y = expressionUsingX x
    let! z = expressionUsingY y
    return x+y+z }

In Haskell, the equivalent is the “do notation”:

do
    x <- initialExpression
    y <- expressionUsingX x
    z <- expressionUsingY y
    return x+y+z

And in Scala, the equivalent is the “for comprehension”:

for {
    x <- initialExpression
    y <- expressionUsingX(x)
    z <- expressionUsingY(y)
} yield {
    x+y+z
}

It’s important to emphasize that you do not have to use the special syntax when using bind/return. You can always use bind or >>= in the same way as any other function.

The combination of bind and return are considered even more powerful than apply and return, because if you have bind and return, you can construct map and apply from them, but not vice versa.

Here’s how bind can be used to emulate map, for example:

• First, you construct a world-crossing function from a normal function by applying return to the output.
• Next, convert this world-crossing function into a lifted function using bind. This gives you the same result as if you had simply done map in the first place.

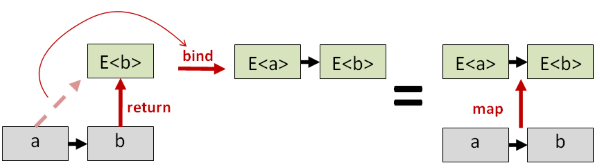
Similarly, bind can emulate apply. Here is how map and apply can be defined using bind and return for Options in F#:

// map defined in terms of bind and return (Some)
let map f =
    Option.bind (f >> Some)

// apply defined in terms of bind and return (Some)
let apply fOpt xOpt =
    fOpt |> Option.bind (fun f ->
        let map = Option.bind (f >> Some)
        map xOpt)

At this point, people often ask “why should I use apply instead of bind when bind is more powerful?”

The answer is that just because apply can be emulated by bind, doesn’t mean it should be. For example, it is possible to implement apply in a way that cannot be emulated by a bind implementation.

In fact, using apply (“applicative style”) or bind (“monadic style”) can have a profound effect on how your program works! We’ll discuss these two approaches in more detail in part 3 of this post.

As with map, and as with apply/return, a correct implementation of the bind/return pair should have some properties that are true no matter what elevated world we are working with.

There are three so-called “Monad Laws”, and one way of defining a Monad (in the programming sense) is to say that it consists of three things: a generic type constructor E<T> plus a pair of functions (bind and return) that obey the monad laws. This is not the only way to define a monad, and mathematicians typically use a slightly different definition, but this one is most useful to programmers.

Just as with the the Functor and Applicative laws we saw earlier, these laws are quite sensible.

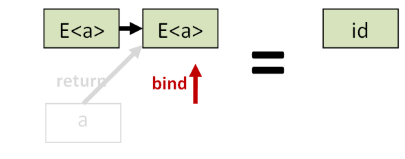
First, note that return function is itself a cross-world function:

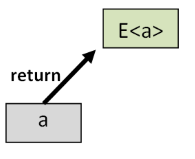
That means that we can use bind to lift it into a function in the elevated world. And what does this lifted function do? Hopefully, nothing! It should just return its input.

So that is exactly the first monad law: it says that this lifted function must be the same as the id function in the elevated world.

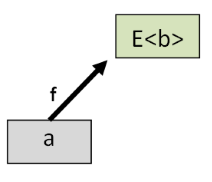
The second law is similar but with bind and return reversed. Say that we have a normal value a and cross-world function f that turns an a into a E<b>.

Let’s lift both of them to the elevated world, using bind on f and return on a.

Now if we apply the elevated version of f to the elevated version of a we get some value E<b>.

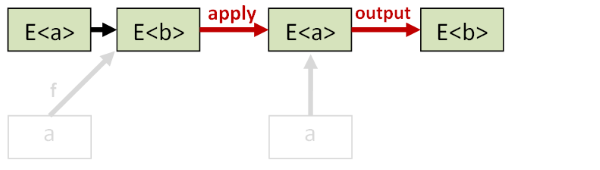
On the other hand if we apply the normal version of f to the normal version of a we also get some value E<b>.

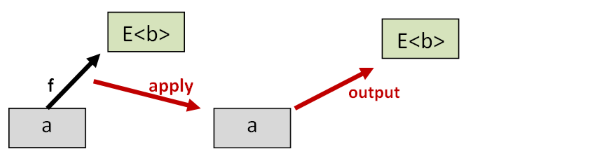
The second monad law says that these two elevated values (E<b>) should be the same. In other words, all this binding and returning should not distort the data.

The third monad law is about associativity.

In the normal world, function composition is associative. For example, we could pipe a value into a function f and then take that result and pipe it into another function g. Alternatively, we can compose f and g first into a single function and then pipe a into it.

let groupFromTheLeft = (a |> f) |> g
let groupFromTheRight = a |> (f >> g)

In the normal world, we expect both of these alternatives to give the same answer.

The third monad law says that, after using bind and return, the grouping doesn’t matter either. The two examples below correspond to the examples above:

let groupFromTheLeft = (a >>= f) >>= g
let groupFromTheRight = a >>= (fun x -> f x >>= g)

And again, we expect both of these to give the same answer.

If you look at the definition above, a monad has a type constructor (a.k.a “generic type”) and two functions and a set of properties that must be satisfied.

The List data type is therefore just one component of a monad, as is the Option data type. List and Option, by themselves, are not monads.

It might be better to think of a monad as a transformation, so that the “List monad” is the transformation that converts the normal world to the elevated “List world”, and the “Option monad” is the transformation that converts the normal world to the elevated “Option world”.

I think this is where a lot of the confusion comes in. The word “List” can mean many different things:

1. A concrete type or data structure such as List<int>.
2. A type constructor (generic type): List<T>.
3. A type constructor and some operations, such as a List class or module.
4. A type constructor and some operations and the operations satisfy the monad laws.

Only the last one is a monad! The other meanings are valid but contribute to the confusion.

Also the last two cases are hard to tell apart by looking at the code. Unfortunately, there have been cases where implementations did not satisfy the monad laws. Just because it’s a “Monad” doesn’t mean that it’s a monad.

Personally, I try to avoid using the word “monad” on this site and focus on the bind function instead, as part of a toolkit of functions for solving problems rather than an abstract concept.

So don’t ask: Do I have a monad?

Do ask: Do I have useful bind and return functions? And are they implemented correctly?

We now have a set of four core functions: map, return, apply, and bind, and I hope that you are clear on what each one does.

But there are some questions that have not been addressed yet, such as “why should I choose apply instead of bind?”, or “how can I deal with multiple elevated worlds at the same time?”

In the next post we’ll address these questions and demonstrate how to use the toolset with a series of practical examples.

UPDATE: Fixed error in monad laws pointed out by @joseanpg. Thanks!