Railway oriented programming

UPDATE: Slides and video from a more comprehensive presentation available here (and if you understand the Either monad, read this first!).

UPDATE 2: This is one of my most popular posts, and it is a useful approach to error handling, but please don’t overuse the idea! See my post on “Against Railway-Oriented Programming”.

In the previous post, we saw how a use case could be broken into steps, and all the errors shunted off onto a separate error track, like this:

In this post, we’ll look at various ways of connecting these step functions into a single unit. The detailed internal design of the functions will be described in a later post.

Let’s have a closer look at these steps. For example, consider the validation function. How would it work? Some data goes in, but what comes out?

Well, there are two possible cases: either the data is valid (the happy path), or something is wrong, in which case we go onto the failure path and bypass the rest of the steps, like this:

But as before, this would not be a valid function. A function can only have one output, so we must use the Result type we defined last time:

type Result<'TSuccess,'TFailure> =
    | Success of 'TSuccess
    | Failure of 'TFailure

And the diagram now looks like this:

To show you how this works in practice, here is an example of what an actual validation function might look like:

type Request = {name:string; email:string}

let validateInput input =
   if input.name = "" then Failure "Name must not be blank"
   else if input.email = "" then Failure "Email must not be blank"
   else Success input  // happy path

If you look at the type of the function, the compiler has deduced that it takes a Request and spits out a Result as output, with a Request for the success case and a string for the failure case:

validateInput : Request -> Result<Request,string>

We can analyze the other steps in the flow in the same way. We will find that each one will have the same “shape” – some sort of input and then this Success/Failure output.

A pre-emptive apology: Having just said that a function can’t have two outputs, I may occasionally refer to them hereafter as “two output” functions! Of course, what I mean is that the shape of the function output has two cases.

So we have a lot of these “one input -> Success/Failure output” functions – how do we connect them together?

What we want to do is connect the Success output of one to the input of the next, but somehow bypass the second function in case of a Failure output. This diagram gives the general idea:

There is a great analogy for doing this – something you are probably already familiar with. Railways!

Railways have switches (“points” in the UK) for directing trains onto a different track. We can think of these “Success/Failure” functions as railway switches, like this:

And here we have two in a row.

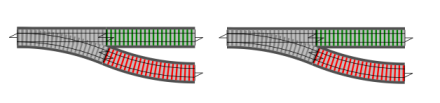
How do we combine them so that both failure tracks are connected? It’s obvious – like this!

And if we have a whole series of switches, we will end up with a two track system, looking something like this:

The top track is the happy path, and the bottom track is the failure path.

Now stepping back and looking at the big picture, we can see that we will have a series of black box functions that appear to be straddling a two-track railway, each function processing data and passing it down the track to the next function:

But if we look inside the functions, we can see that there is actually a switch inside each one, for shunting bad data onto the failure track:

Note that once we get on the failure path, we never (normally) get back onto the happy path. We just bypass the rest of the functions until we reach the end.

Before we discuss how to “glue” the step functions together, let’s review how composition works.

Imagine that a standard function is a black box (a tunnel, say) sitting on a one-track railway. It has one input and one output.

If we want to connect a series of these one-track functions, we can use the left-to-right composition operator, with the symbol >>.

The same composition operation also works with two-track functions as well:

The only constraint on composition is that the output type of the left-hand function has to match the input type of the right-hand function.

In our railway analogy, this means that you can connect one-track output to one-track input, or two-track output to two-track input, but you can’t directly connect two-track output to one-track input.

So now we have run into a problem.

The function for each step is going to be a switch, with one input track. But the overall flow requires a two-track system, with each function straddling both tracks, meaning that each function must have a two-track input (the Result output by the previous function), not just a simple one-track input (Request).

How can we insert the switches into the two track system?

The answer is simple. We can create an “adapter” function that has a “hole” or “slot” for a switch function and converts it into a proper two-track function. Here’s an illustration:

And here’s what the actual code looks like. I’m going to name the adapter function bind, which is the standard name for it.

let bind switchFunction =
    fun twoTrackInput ->
        match twoTrackInput with
        | Success s -> switchFunction s
        | Failure f -> Failure f

The bind function takes a switch function as a parameter and returns a new function. The new function takes a two-track input (which is of type Result) and then checks each case. If the input is a Success it calls the switchFunction with the value. But if the input is a Failure, then the switch function is bypassed.

Compile it and then look at the function signature:

val bind : ('a -> Result<'b,'c>) -> Result<'a,'c> -> Result<'b,'c>

One way of interpreting this signature is that the bind function has one parameter, a switch function ('a -> Result<..>) and it returns a fully two-track function (Result<..> -> Result<..>) as output.

To be even more specific:

• The parameter (switchFunction) of bind takes some type 'a and emits a Result of type 'b (for the success track) and 'c (for the failure track)
• The returned function itself has a parameter (twoTrackInput) which is a Result of type 'a (for success) and 'c (for failure). The type 'a has to be the same as what the switchFunction is expecting on its one track.
• The output of the returned function is another Result, this time of type 'b (for success) and 'c (for failure) – the same type as the switch function output.

If you think about it, this type signature is exactly what we would expect.

Note that this function is completely generic – it will work with any switch function and any types. All it cares about is the “shape” of the switchFunction, not the actual types involved.

Just as an aside, there are some other ways of writing functions like this.

One way is to use an explicit second parameter for the twoTrackInput rather than defining an internal function, like this:

let bind switchFunction twoTrackInput =
    match twoTrackInput with
    | Success s -> switchFunction s
    | Failure f -> Failure f

This is exactly the same as the first definition. And if you are wondering how a two parameter function can be exactly the same as a one parameter function, you need to read the post on currying!

Yet another way of writing it is to replace the match..with syntax with the more concise function keyword, like this:

let bind switchFunction =
    function
    | Success s -> switchFunction s
    | Failure f -> Failure f

You might see all three styles in other code, but I personally prefer to use the second style (let bind switchFunction twoTrackInput = ), because I think that having explicit parameters makes the code more readable for non-experts.

If you like my way of explaining things with pictures, take a look at my "Domain Modeling Made Functional" book! It's a friendly introduction to Domain Driven Design, modeling with types, and functional programming.

Let’s write a little bit of code now, to test the concepts.

Let’s start with what we already have defined. Request, Result and bind:

type Result<'TSuccess,'TFailure> =
    | Success of 'TSuccess
    | Failure of 'TFailure

type Request = {name:string; email:string}

let bind switchFunction twoTrackInput =
    match twoTrackInput with
    | Success s -> switchFunction s
    | Failure f -> Failure f

Next we’ll create three validation functions, each of which is a “switch” function, with the goal of combining them into one bigger function:

let validate1 input =
   if input.name = "" then Failure "Name must not be blank"
   else Success input

let validate2 input =
   if input.name.Length > 50 then Failure "Name must not be longer than 50 chars"
   else Success input

let validate3 input =
   if input.email = "" then Failure "Email must not be blank"
   else Success input

Now to combine them, we apply bind to each validation function to create a new alternative function that is two-tracked.

Then we can connect the two-tracked functions using standard function composition, like this:

/// glue the three validation functions together
let combinedValidation =
    // convert from switch to two-track input
    let validate2' = bind validate2
    let validate3' = bind validate3
    // connect the two-tracks together
    validate1 >> validate2' >> validate3'

The functions validate2' and validate3' are new functions that take two-track input. If you look at their signatures you will see that they take a Result and return a Result. But note that validate1 does not need to be converted to two track input. Its input is left as one-track, and its output is two-track already, as needed for composition to work.

Here’s a diagram showing the Validate1 switch (unbound) and the Validate2 and Validate3 switches, together with the Validate2' and Validate3' adapters.

We could have also “inlined” the bind, like this:

let combinedValidation =
    // connect the two-tracks together
    validate1
    >> bind validate2
    >> bind validate3

Let’s test it with two bad inputs and a good input:

// test 1
let input1 = {name=""; email=""}
combinedValidation input1
|> printfn "Result1=%A"

// ==> Result1=Failure "Name must not be blank"

// test 2
let input2 = {name="Alice"; email=""}
combinedValidation input2
|> printfn "Result2=%A"

// ==> Result2=Failure "Email must not be blank"

// test 3
let input3 = {name="Alice"; email="good"}
combinedValidation input3
|> printfn "Result3=%A"

// ==> Result3=Success {name = "Alice"; email = "good";}

I would encourage you to try it for yourself and play around with the validation functions and test input.

You might be wondering if there is a way to run all three validations in parallel, rather than serially, so that you can get back all the validation errors at once. Yes, there is a way, which I’ll explain later in this post.

While we are discussing the bind function, there is a common symbol for it, >>=, which is used to pipe values into switch functions.

Here’s the definition, which switches around the two parameters to make them easier to chain together:

/// create an infix operator
let (>>=) twoTrackInput switchFunction =
    bind switchFunction twoTrackInput

One way to remember the symbol is to think of it as the composition symbol, >>, followed by a two-track railway symbol, =.

When used like this, the >>= operator is sort of like a pipe (|>) but for switch functions.

In a normal pipe, the left hand side is a one-track value, and the right hand value is a normal function. But in a “bind pipe” operation, the left hand side is a two-track value, and the right hand value is a switch function.

Here it is in use to create another implementation of the combinedValidation function.

let combinedValidation x =
    x
    |> validate1   // normal pipe because validate1 has a one-track input
                   // but validate1 results in a two track output...
    >>= validate2  // ... so use "bind pipe". Again the result is a two track output
    >>= validate3   // ... so use "bind pipe" again.

The difference between this implementation and the previous one is that this definition is data-oriented rather than function-oriented. It has an explicit parameter for the initial data value, namely x. x is passed to the first function, and then the output of that is passed to the second function, and so on.

In the previous implementation (repeated below), there was no data parameter at all! The focus was on the functions themselves, not the data that flows through them.

let combinedValidation =
    validate1
    >> bind validate2
    >> bind validate3

Another way to combine switches is not by adapting them to a two track input, but simply by joining them directly together to make a new, bigger switch.

In other words, this:

becomes this:

But if you think about it, this combined track is actually just another switch! You can see this if you cover up the middle bit. There’s one input and two outputs:

So what we have really done is a form of composition for switches, like this:

Because each composition results in just another switch, we can always add another switch again, resulting in an even bigger thing that is still a switch, and so on.

Here’s the code for switch composition. The standard symbol used is >=>, a bit like the normal composition symbol, but with a railway track between the angles.

let (>=>) switch1 switch2 x =
    match switch1 x with
    | Success s -> switch2 s
    | Failure f -> Failure f

Again, the actual implementation is very straightforward. Pass the single track input x through the first switch. On success, pass the result into the second switch, otherwise bypass the second switch completely.

Now we can rewrite the combinedValidation function to use switch composition rather than bind:

let combinedValidation =
    validate1
    >=> validate2
    >=> validate3

This one is the simplest yet, I think. It’s very easy to extend of course, if we have a fourth validation function, we can just append it to the end.

We have two different concepts that at first glance seem quite similar. What’s the difference?

To recap:

• Bind has one switch function parameter. It is an adapter that converts the switch function into a fully two-track function (with two-track input and two-track output).
• Switch composition has two switch function parameters. It combines them in series to make another switch function.

So why would you use bind rather than switch composition? It depends on the context. If you have an existing two-track system, and you need to insert a switch, then you have to use bind as an adapter to convert the switch into something that takes two-track input.

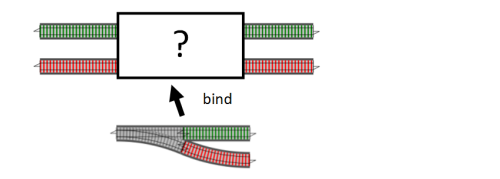
On the other hand, if your entire data flow consists of a chain of switches, then switch composition can be simpler.

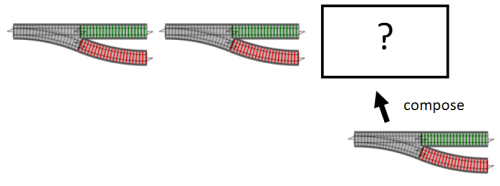
As it happens, switch composition can be written in terms of bind. If you connect the first switch with a bind-adapted second switch, you get the same thing as switch composition:

Here are two separate switches:

And then here are the switches composed together to make a new bigger switch:

And here’s the same thing done by using bind on the second switch:

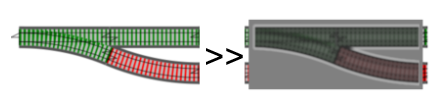
Here’s the switch composition operator rewritten using this way of thinking:

let (>=>) switch1 switch2 =
    switch1 >> (bind switch2)

This implementation of switch composition is much simpler than the first one, but also more abstract. Whether it is easier to comprehend for a beginner is another matter! I find that if you think of functions as things in their own right, rather than just as conduits for data, this approach becomes easier to understand.

Once you get the hang of it, you can fit all sorts of other things into this model.

For example, let’s say we have a function that is not a switch, just a regular function. And say that we want to insert it into our flow.

Here’s a real example - say that we want to trim and lowercase the email address after the validation is complete. Here’s some code to do this:

let canonicalizeEmail input =
   { input with email = input.email.Trim().ToLower() }

This code takes a (single-track) Request and returns a (single-track) Request.

How can we insert this after the validation steps but before the update step?

Well, if we can turn this simple function into a switch function, then we can use the switch composition we just talked about above.

In other words, we need an adapter block. It has the same concept that we used for bind, except that this time our adapter block will have a slot for one-track function, and the overall “shape” of the adapter block is a switch.

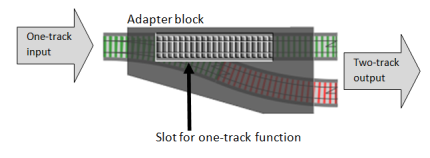
The code to do this is trivial. All we need to do is take the output of the one track function and turn it into a two-track result. In this case, the result will always be Success.

// convert a normal function into a switch
let switch f x =
    f x |> Success

In railway terms, we have added a bit of failure track. Taken as a whole, it looks like a switch function (one-track input, two-track output), but of course, the failure track is just a dummy and the switch never actually gets used.

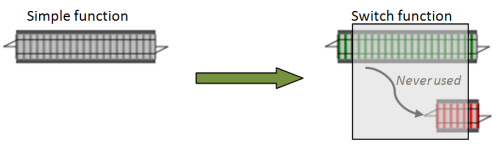
Once switch is available, we can easily append the canonicalizeEmail function to the end of the chain. Since we are beginning to extend it, let’s rename the function to usecase.

let usecase =
    validate1
    >=> validate2
    >=> validate3
    >=> switch canonicalizeEmail

Try testing it to see what happens:

let goodInput = {name="Alice"; email="UPPERCASE   "}
usecase goodInput
|> printfn "Canonicalize Good Result = %A"

//Canonicalize Good Result = Success {name = "Alice"; email = "uppercase";}

let badInput = {name=""; email="UPPERCASE   "}
usecase badInput
|> printfn "Canonicalize Bad Result = %A"

//Canonicalize Bad Result = Failure "Name must not be blank"

In the previous example, we took a one-track function and created a switch from it. This enabled us to use switch composition with it.

Sometimes though, you want to use the two-track model directly, in which case you want to turn a one-track function into a two-track function directly.

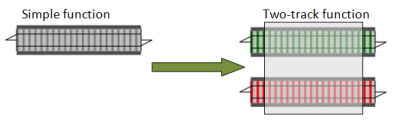
Again, we just need an adapter block with a slot for the simple function. We typically call this adapter map.

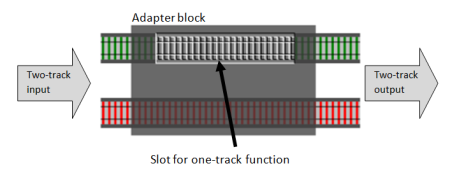
And again, the actual implementation is very straightforward. If the two-track input is Success, call the function, and turn its output into Success. On the other hand, if the two-track input is Failure bypass the function completely.

Here’s the code:

// convert a normal function into a two-track function
let map oneTrackFunction twoTrackInput =
    match twoTrackInput with
    | Success s -> Success (oneTrackFunction s)
    | Failure f -> Failure f

And here it is in use with canonicalizeEmail:

let usecase =
    validate1
    >=> validate2
    >=> validate3
    >> map canonicalizeEmail  // normal composition

Note that normal composition is now used because map canonicalizeEmail is a fully two-track function and can be connected to the output of the validate3 switch directly.

In other words, for one-track functions, >=> switch is exactly the same as >> map. Your choice.

Another function we will often want to work with is a “dead-end” function – a function that accepts input but has no useful output.

For example, consider a function that updates a database record. It is useful only for its side-effects – it doesn’t normally return anything.

How can we incorporate this kind of function into the flow?

What we need to do is:

• Save a copy of the input.
• Call the function and ignore its output, if any.
• Return the original input for passing on to the next function in the chain.

From a railway point of view, this is equivalent to creating a dead-end siding, like this.

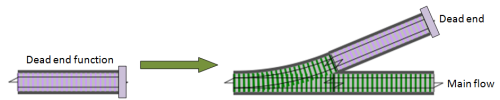
To make this work, we need another adapter function, like switch, except that this time it has a slot for one-track dead-end function, and converts it into a single-track pass through function, with a one-track output.

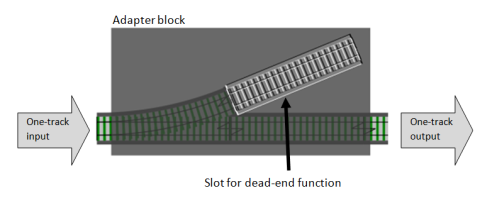
Here’s the code, which I will call tee, after the UNIX tee command:

let tee f x =
    f x |> ignore
    x

Once we have converted the dead-end function to a simple one-track pass through function, we can then use it in the data flow by converting it using switch or map as described above.

Here’s the code in use with the “switch composition” style:

// a dead-end function
let updateDatabase input =
   ()   // dummy dead-end function for now

let usecase =
    validate1
    >=> validate2
    >=> validate3
    >=> switch canonicalizeEmail
    >=> switch (tee updateDatabase)

Or alternatively, rather than using switch and then connecting with >=>, we can use map and connect with >>.

Here’s a variant implementation which is exactly the same but uses the “two-track” style with normal composition

let usecase =
    validate1
    >> bind validate2
    >> bind validate3
    >> map canonicalizeEmail
    >> map (tee updateDatabase)

Our dead end database update might not return anything, but that doesn’t mean that it might not throw an exception. Rather than crashing, we want to catch that exception and turn it into a failure.

The code is similar to the switch function, except that it catches exceptions. I’ll call it tryCatch:

let tryCatch f x =
    try
        f x |> Success
    with
    | ex -> Failure ex.Message

And here is a modified version of the data flow, using tryCatch rather than switch for the update database code.

let usecase =
    validate1
    >=> validate2
    >=> validate3
    >=> switch canonicalizeEmail
    >=> tryCatch (tee updateDatabase)

All the functions we have seen so far have only one input, because they always just work with data travelling along the happy path.

Sometimes though, you do need a function that handles both tracks. For example, a logging function that logs errors as well as successes.

As we have done previously, we will create an adapter block, but this time it will have slots for two separate one-track functions.

Here’s the code:

let doubleMap successFunc failureFunc twoTrackInput =
    match twoTrackInput with
    | Success s -> Success (successFunc s)
    | Failure f -> Failure (failureFunc f)

As an aside, we can use this function to create a simpler version of map, using id for the failure function:

let map successFunc =
    doubleMap successFunc id

Let’s use doubleMap to insert some logging into the data flow:

let log twoTrackInput =
    let success x = printfn "DEBUG. Success so far: %A" x; x
    let failure x = printfn "ERROR. %A" x; x
    doubleMap success failure twoTrackInput

let usecase =
    validate1
    >=> validate2
    >=> validate3
    >=> switch canonicalizeEmail
    >=> tryCatch (tee updateDatabase)
    >> log

Here’s some test code, with the results:

let goodInput = {name="Alice"; email="good"}
usecase goodInput
|> printfn "Good Result = %A"

// DEBUG. Success so far: {name = "Alice"; email = "good";}
// Good Result = Success {name = "Alice"; email = "good";}

let badInput = {name=""; email=""}
usecase badInput
|> printfn "Bad Result = %A"

// ERROR. "Name must not be blank"
// Bad Result = Failure "Name must not be blank"

For completeness, we should also create simple functions that turn a single simple value into a two-track value, either success or failure.

let succeed x =
    Success x

let fail x =
    Failure x

Right now these are trivial, just calling the constructor of the Result type, but when we get down to some proper coding we’ll see that by using these rather than the union case constructor directly, we can isolate ourselves from changes behind the scenes.

So far, we have combined functions in series. But with something like validation, we might want to run multiple switches in parallel, and combine the results, like this:

To make this easier, we can reuse the same trick that we did for switch composition. Rather than doing many at once, if we just focus on a single pair, and “add” them to make a new switch, we can then easily chain the “addition” together so that we can add as many as we want. In other words, we just need to implement this:

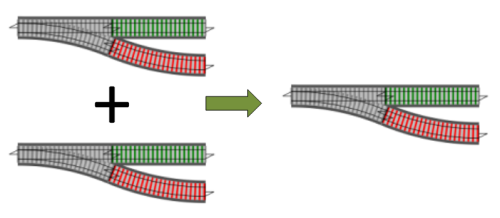
So, what is the logic for adding two switches in parallel?

• First, take the input and apply it to each switch.
• Next look at the outputs of both switches, and if both are successful, the overall result is Success.
• If either output is a failure, then the overall result is Failure as well.

Here’s the function, which I will call plus:

let plus switch1 switch2 x =
    match (switch1 x),(switch2 x) with
    | Success s1,Success s2 -> Success (s1 + s2)
    | Failure f1,Success _  -> Failure f1
    | Success _ ,Failure f2 -> Failure f2
    | Failure f1,Failure f2 -> Failure (f1 + f2)

But we now have a new problem. What do we do with two successes, or two failures? How do we combine the inner values?

I used s1 + s2 and f1 + f2 in the example above, but that implies that there is some sort of + operator we can use. That may be true for strings and ints, but it is not true in general.

The method of combining values might change in different contexts, so rather than trying to solve it once and for all, let’s punt by letting the caller pass in the functions that are needed.

Here’s a rewritten version:

let plus addSuccess addFailure switch1 switch2 x =
    match (switch1 x),(switch2 x) with
    | Success s1,Success s2 -> Success (addSuccess s1 s2)
    | Failure f1,Success _  -> Failure f1
    | Success _ ,Failure f2 -> Failure f2
    | Failure f1,Failure f2 -> Failure (addFailure f1 f2)

I have put these new functions first in the parameter list, to aid partial application.

Now let’s create a implementation of “plus” for the validation functions.

• When both functions succeed, they will return the request unchanged, so the addSuccess function can return either parameter.
• When both functions fail, they will return different strings, so the addFailure function should concatenate them.

For validation then, the “plus” operation that we want is like an “AND” function. Only if both parts are “true” is the result “true”.

That naturally leads to wanting to use && as the operator symbol. Unfortunately, && is reserved, but we can use &&&, like this:

// create a "plus" function for validation functions
let (&&&) v1 v2 =
    let addSuccess r1 r2 = r1 // return first
    let addFailure s1 s2 = s1 + "; " + s2  // concat
    plus addSuccess addFailure v1 v2

And now using &&&, we can create a single validation function that combines the three smaller validations:

let combinedValidation =
    validate1
    &&& validate2
    &&& validate3

Now let’s try it with the same tests we had earlier:

// test 1
let input1 = {name=""; email=""}
combinedValidation input1
|> printfn "Result1=%A"
// ==>  Result1=Failure "Name must not be blank; Email must not be blank"

// test 2
let input2 = {name="Alice"; email=""}
combinedValidation input2
|> printfn "Result2=%A"
// ==>  Result2=Failure "Email must not be blank"

// test 3
let input3 = {name="Alice"; email="good"}
combinedValidation input3
|> printfn "Result3=%A"
// ==>  Result3=Success {name = "Alice"; email = "good";}

The first test now has two validation errors combined into a single string, just as we wanted.

Next, we can tidy up the main dataflow function by using the usecase function now instead of the three separate validation functions we had before:

let usecase =
    combinedValidation
    >=> switch canonicalizeEmail
    >=> tryCatch (tee updateDatabase)

And if we test that now, we can see that a success flows all the way to the end and that the email is lowercased and trimmed:

// test 4
let input4 = {name="Alice"; email="UPPERCASE   "}
usecase input4
|> printfn "Result4=%A"
// ==>  Result4=Success {name = "Alice"; email = "uppercase";}

You might be asking, can we create a way of OR-ing validation functions as well? That is, the overall result is valid if either part is valid? The answer is yes, of course. Try it! I suggest that you use the symbol ||| for this.

Another thing we might want to do is add or remove functions into the flow dynamically, based on configuration settings, or even the content of the data.

The simplest way to do this is to create a two-track function to be injected into the stream, and replace it with the id function if not needed.

Here’s the idea:

let injectableFunction =
    if config.debug then debugLogger else id

Let’s try it with some real code:

type Config = {debug:bool}

let debugLogger twoTrackInput =
    let success x = printfn "DEBUG. Success so far: %A" x; x
    let failure = id // don't log here
    doubleMap success failure twoTrackInput

let injectableLogger config =
    if config.debug then debugLogger else id

let usecase config =
    combinedValidation
    >> map canonicalizeEmail
    >> injectableLogger config

And here is it in use:

let input = {name="Alice"; email="good"}

let releaseConfig = {debug=false}
input
|> usecase releaseConfig
|> ignore

// no output

let debugConfig = {debug=true}
input
|> usecase debugConfig
|> ignore

// debug output
// DEBUG. Success so far: {name = "Alice"; email = "good";}

Let’s step back and review what we have done so far.

Using railway track as a metaphor, we have created a number of useful building blocks that will work with any data-flow style application.

We can classify our functions roughly like this:

• “constructors” are used to create new track.
• “adapters” convert one kind of track into another.
• “combiners” link sections of track together to make a bigger piece of track.

These functions form what can be loosely called a combinator library, that is, a group of functions that are designed to work with a type (here represented by railway track), with the design goal that bigger pieces can be built by adapting and combining smaller pieces.

Functions like bind, map, plus, etc., crop up in all sorts of functional programming scenarios, and so you can think of them as functional patterns – similar to, but not the same as, the OO patterns such as “visitor”, “singleton”, “facade”, etc.

Here they all are together:

Here is the complete code for all the functions in one place.

I have made some minor tweaks from the original code presented above:

• Most functions are now defined in terms of a core function called either.
• tryCatch has been given an extra parameter for the exception handler.

// the two-track type
type Result<'TSuccess,'TFailure> =
    | Success of 'TSuccess
    | Failure of 'TFailure

// convert a single value into a two-track result
let succeed x =
    Success x

// convert a single value into a two-track result
let fail x =
    Failure x

// apply either a success function or failure function
let either successFunc failureFunc twoTrackInput =
    match twoTrackInput with
    | Success s -> successFunc s
    | Failure f -> failureFunc f

// convert a switch function into a two-track function
let bind f =
    either f fail

// pipe a two-track value into a switch function
let (>>=) x f =
    bind f x

// compose two switches into another switch
let (>=>) s1 s2 =
    s1 >> bind s2

// convert a one-track function into a switch
let switch f =
    f >> succeed

// convert a one-track function into a two-track function
let map f =
    either (f >> succeed) fail

// convert a dead-end function into a one-track function
let tee f x =
    f x; x

// convert a one-track function into a switch with exception handling
let tryCatch f exnHandler x =
    try
        f x |> succeed
    with
    | ex -> exnHandler ex |> fail

// convert two one-track functions into a two-track function
let doubleMap successFunc failureFunc =
    either (successFunc >> succeed) (failureFunc >> fail)

// add two switches in parallel
let plus addSuccess addFailure switch1 switch2 x =
    match (switch1 x),(switch2 x) with
    | Success s1,Success s2 -> Success (addSuccess s1 s2)
    | Failure f1,Success _  -> Failure f1
    | Success _ ,Failure f2 -> Failure f2
    | Failure f1,Failure f2 -> Failure (addFailure f1 f2)

So far, we have focused entirely on the shape of the track, not the cargo on the trains.

This is a magical railway, where the goods being carried can change as they go along each length of track.

For example, a cargo of pineapples will magically transform into apples when it goes through the tunnel called function1.

And a cargo of apples will transform into bananas when it goes through the tunnel called function2.

This magical railway has an important rule, namely that you can only connect tracks which carry the same type of cargo. In this case we can connect function1 to function2 because the cargo coming out of function1 (apples) is the same as the cargo going into function2 (also apples).

Of course, it is not always true that the tracks carry the same cargo, and a mismatch in the kind of cargo will cause an error.

But you’ll notice that in this discussion so far, we haven’t mentioned the cargo once! Instead, we have spent all our time talking about one-track vs. two track functions.

Of course, it goes without saying that the cargo must match up. But I hope you can see that it is the shape of the track that is really the important thing, not the cargo that is carried.

Why have we not worried about the type of cargo? Because all the “adapter” and “combiner” functions are completely generic! The bind and map and switch and plus functions do not care about the type of the cargo, only the shape of the track.

Having extremely generic functions is a benefit in two ways. The first way is obvious: the more generic a function is, the more reusable it is. The implementation of bind will work with any types (as long as the shape is right).

But there is another, more subtle aspect of generic functions that is worth pointing out. Because we generally know nothing about the types involved, we are very constrained in what we can and can’t do. As a result, we can’t introduce bugs!

To see what I mean, let’s look at the signature for map:

val map : ('a -> 'b) -> (Result<'a,'c> -> Result<'b,'c>)

It takes a function parameter 'a -> 'b and a value Result<'a,'c> and returns a value Result<'b,'c>.

We don’t know anything about the types 'a, 'b, and 'c. The only things we know are that:

• The same type 'a shows up in both the function parameter and the Success case of the first Result.
• The same type 'b shows up in both the function parameter and the Success case of the second Result.
• The same type 'c shows up in the Failure cases of both the first and second Results, but doesn’t show up in the function parameter at all.

What can we deduce from this?

The return value has a type 'b in it. But where does it come from? We don’t know what type 'b is, so we don’t know how to make one. But the function parameter knows how to make one! Give it an 'a and it will make a 'b for us.

But where can we get an 'a from? We don’t know what type 'a is either, so again we don’t know how to make one. But the first result parameter has an 'a we can use, so you can see that we are forced to get the Success value from the Result<'a,'c> parameter and pass it to the function parameter. And then the Success case of the Result<'b,'c> return value must be constructed from the result of the function.

Finally, the same logic applies to 'c. We are forced to get the Failure value from the Result<'a,'c> input parameter and use it to construct the Failure case of the Result<'a,'c> return value.

In other words, there is basically only one way to implement the map function! The type signature is so generic that we have no choice.

On the other hand, imagine that the map function had been very specific about the types it needed, like this:

val map : (int -> int) -> (Result<int,int> -> Result<int,int>)

In this case, we can come up a huge number of different implementations. To list a few:

• We could have swapped the success and failure tracks.
• We could have added a random number to the success track.
• We could have ignored the function parameter altogether, and returned zero on both the success and failure tracks.

All of these implementations are “buggy” in the sense that they don’t do what we expect. But they are all only possible because we know in advance that the type is int, and therefore we can manipulate the values in ways we are not supposed to. The less we know about the types, the less likely we are to make a mistake.

In most of our functions, the transformation only applies to the success track. The failure track is left alone (map), or merged with an incoming failure (bind).

This implies that the failure track must be same type all the way through. In this post we have just used string, but in the next post we’ll change the failure type to be something more useful.

At the beginning of this series, I promised to give you a simple recipe that you could follow.

But you might be feeling a bit overwhelmed now. Instead of making things simpler, I seem to have made things more complicated. I have shown you lots of different ways of doing the same thing! Bind vs. compose. Map vs. switch. Which approach should you use? Which way is best?

Of course, there is never one “right way” for all scenarios, but nevertheless, as promised, here are some guidelines that can be used as the basis of a reliable and repeatable recipe.

Guidelines

• Use double-track railway as your underlying model for dataflow situations.
• Create a function for each step in the use case. The function for each step can in turn be built from smaller functions (e.g. the validation functions).
• Use standard composition (>>) to connect the functions.
• If you need to insert a switch into the flow, use bind.
• If you need to insert a single-track function into the flow, use map.
• If you need to insert other types of functions into the flow, create an appropriate adapter block and use it.

These guidelines may result in code that is not particularly concise or elegant, but on the other hand, you will be using a consistent model, and it should be understandable to other people when it needs to be maintained.

So with these guidelines, here are the main bits of the implementation so far. Note especially the use of >> everywhere in the final usecase function.

open RailwayCombinatorModule

let (&&&) v1 v2 =
    let addSuccess r1 r2 = r1 // return first
    let addFailure s1 s2 = s1 + "; " + s2  // concat
    plus addSuccess addFailure v1 v2

let combinedValidation =
    validate1
    &&& validate2
    &&& validate3

let canonicalizeEmail input =
   { input with email = input.email.Trim().ToLower() }

let updateDatabase input =
   ()   // dummy dead-end function for now

// new function to handle exceptions
let updateDatebaseStep =
    tryCatch (tee updateDatabase) (fun ex -> ex.Message)

let usecase =
    combinedValidation
    >> map canonicalizeEmail
    >> bind updateDatebaseStep
    >> log

One final suggestion. If you are working with a team of non-experts, unfamiliar operator symbols will put people off. So here some extra guidelines with respect to operators:

• Don’t use any “strange” operators other than >> and |>.
• In particular, that means you should not use operators like >>= or >=> unless everyone is aware of them.
• An exception can be made if you define the operator at the top of the module or function where it is used. For example, the &&& operator could be defined at the top of the validation module and then used later in that same module.

• If you like this “railway oriented” approach, you can also see it applied to FizzBuzz.
• I also have some slides and video that show how take this approach further. (At some point I will turn these into a proper blog post)

I presented on this topic at NDC Oslo 2014 (click image to view video)

And here are the slides I used:

If you are interested in the functional approach to domain modelling and design, you might enjoy my "Domain Modeling Made Functional" book! It's a beginner-friendly introduction that covers Domain Driven Design, modeling with types, and functional programming.